Vector Reflection
這篇文應該是要跟MTV(Minimum Translation Vector)的碰撞回饋一起寫,但MTV發起來有點長,懶得打,先記錄Vector Reflection
為什麼需要取得鏡射向量(Vector reflection)
一個簡單的例子,當乒乓球擊中球拍時,要如何取得反彈後的向量,而光影模擬時也會需要取得光線反射的向量,這時向量反射就非常重要了。
因為這篇內容比較基礎,所以一些基本部份就省略了
如何取得Vector reflection
先定義一些資訊:
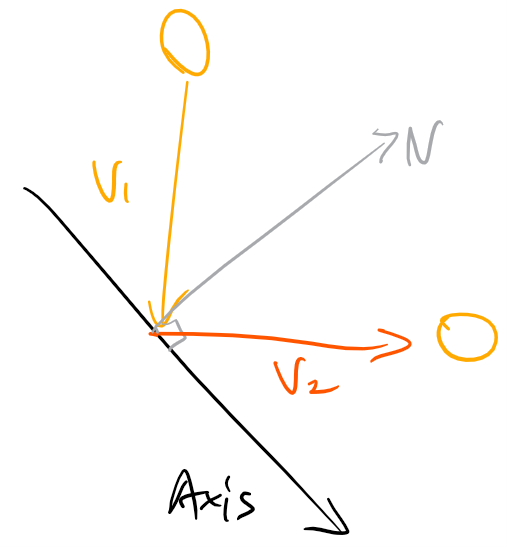
- V1 = 物體的速度
- V2 = 物體反彈後的速度
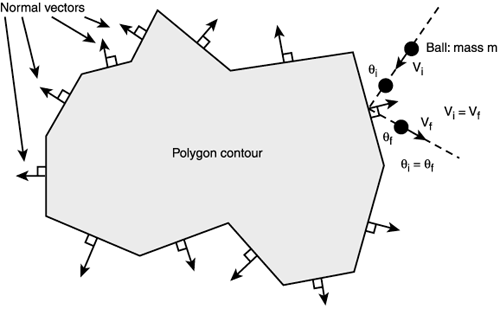
- N = 擊中平面的法向量
如何取得擊中平面的法向量 N 呢?
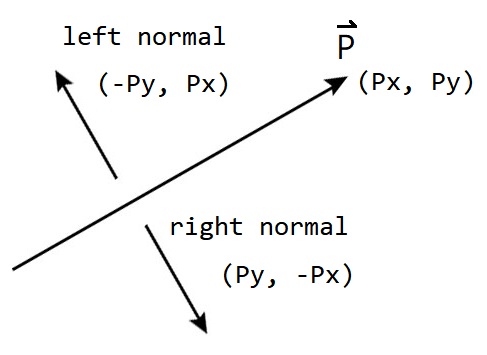
很簡單,透過兩垂直向量點積為0的特性就可以得到,假設Axis是(3, 4)的向量,那平面法向量就會是(-y, x) = (-4, 3) 或是 (y, -x) = (4, -3)
再來看如何取得 V2
將V1與V2之間畫一條線,並組合成一個平行四邊形,這樣就很明顯得到 V2 = 2N' + V1,那麼接下來的問題就會是如何取得N'。
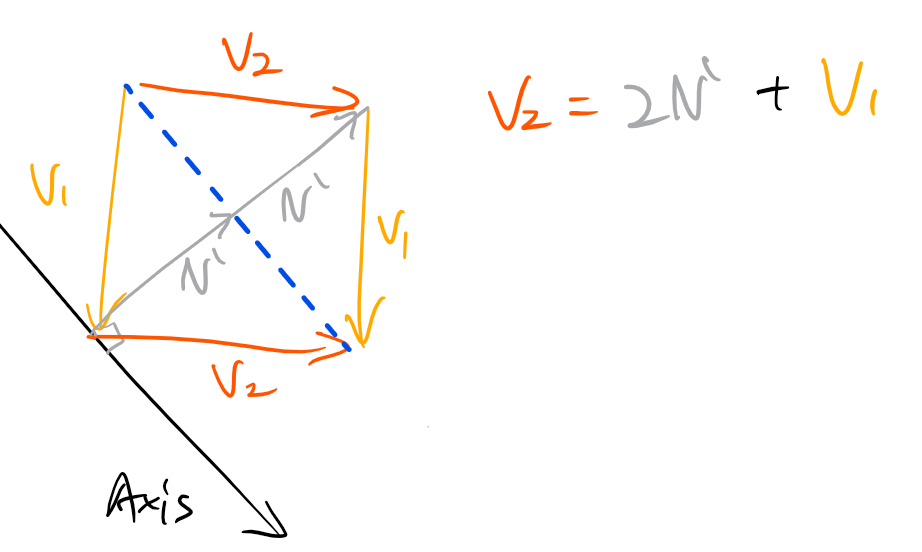
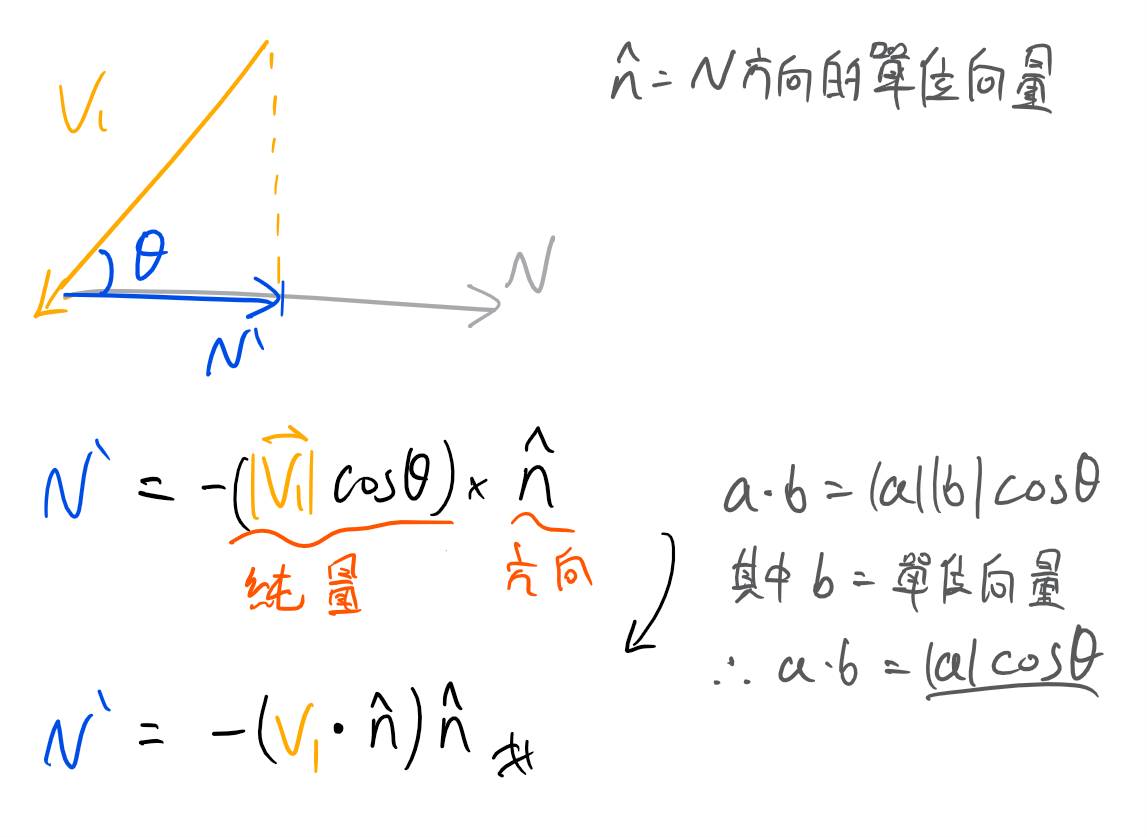
先只單看V1跟法向量N,可以發現N' 其實就是V1在法向量N上面的投影$proj_{\hat n}V_{1}$,所以可以透過基本三角函數來取得
但$\cos \theta$需要另外計算夾角,所以有個更好的方法來代替,在點積公式中,使其中一個向量為單位向量,因為長度為1可直接省略,所以$\left |V_{1} \right | \cos \theta = V_{1} \cdot \hat{n}$,要加負號是因為$V1$與$\hat{n}$為反方向,$\left |V_{1} \right | \cos \theta$會是帶負號的純量,但我們需要的$\hat{n}$是與$V_{1}$反向的,所以加上負號:
而$(V_{1} \cdot \hat{n})\hat{n}$就是快速求得$V_{1}$在法向量$\hat{n}$投影的方式: $$proj_{\hat n}V_{1}=(V_{1} \cdot \hat{n})\hat{n}$$
再來回到$V_{2} = 2N' + V_{1}$
該有的東西都有了,所以整理後可以得到:
$$V_{2} = V_{1} - 2(V_{1} \cdot \hat{n})\hat{n}$$
- V1 = 物體方向
- n = 擊中平面的"單位"法向量
- v2 = 反彈後的方向
接者就可以放在當物體與某個平面碰撞後,更新反彈後的速率為V2,就會有乒乓球反彈的效果了
大概就這樣,具體結果可以參考:從零開始的基礎RPG框架