遊戲中的碰撞檢測Collision Detection

Posted on: 2018-03-21 /
Categories: 程式筆記

應該很多人對電腦遊戲中如何處理碰撞處理感興趣，希望大家在讀完這篇文章後能了解電腦是如何偵測物體的碰撞。

而這篇文有三個主要目的 :

  1. 對遊戲中的碰撞感興趣，卻不會寫程式的人可以了解原理
  2. 讓有能力實作的人，可以跟著文章寫出簡易的多邊形碰撞檢測
  3. 自己的學習筆記

讓我們開始吧。

 

這次要來介紹的主題是分離軸碰撞檢測(Separating Axis Theorem, SAT)

分離軸定理通常用語檢測兩個多邊形或多邊形與圓之間的碰撞，跟所有演算法一樣他具有一定的優勢與缺點。

我會慢慢講解背後的原理，並使用程式碼做簡易的範例。

 

範例所使用的語言為Java Script，加上自製的向量函式庫，但我想觀念懂了應該不會有太大問題。

 

閱讀時建議將頁面拉大一點，一些圖片的呈現會比較清楚。

因為這篇文有點長，在閱讀時請善用目錄連結與下方的Go Top按鈕。

目錄

  1. 矩形碰撞檢測
  2. 什麼是分離軸檢測?
  3. 知識補充1 – 向量
  4. 知識補充2 – 旋轉變換
  5. 如何取得分離軸上的投影?
  6. 編寫程式碼-投影、旋轉與判斷
  7. 如何取得分離軸?
  8. 粗糙的矩形檢測
  9. 編寫程式碼 – 多邊形與多邊形
  10. 編寫程式碼 – 多邊形與圓
  11. SAT的總結
  12. 多物體的碰撞優化
  13. 動態物體間的碰撞檢測
  14. 結尾與感想
  15. 參考資源

 

1. 矩形碰撞檢測

我想先從最簡單的碰撞檢測開始講，這樣比較好讓各位了解為什麼需要分離軸檢測，所以先從一般的矩形碰撞開始。

 

AABB碰撞檢測(Axis-aligned Bounding Box):

為了方邊物體之間進行碰撞檢測運算，通常會對物體創建一個長方形將其包圍，AABB包圍盒也被稱為軸對齊包圍盒。

 

一般二維的AABB包圍盒具備兩項特點:

  1. 以矩形包圍物體
  2. 矩形的每條邊，皆與坐標系的軸垂直

簡單來說就是用矩形把物體包起來，檢查矩形之間是否發生碰撞

 

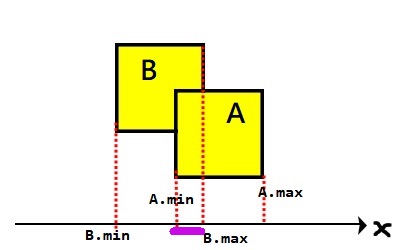
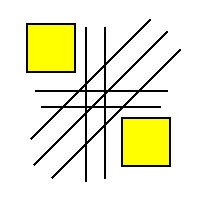
如下圖，黑框及為包圍盒，在做碰撞檢測時，只需要檢查包圍盒之間是否發生碰撞。

那我們就直接來看看AABB碰撞盒是如何運作的吧。

 

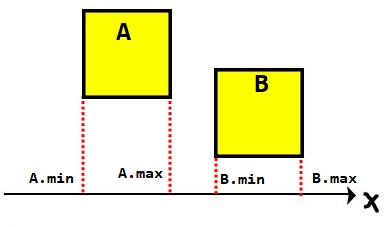
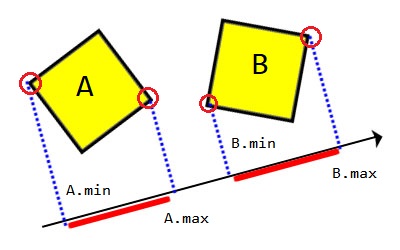
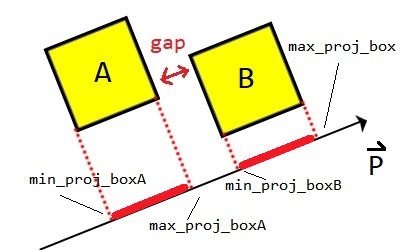
這裡有兩個矩形A、B，Box A最小邊為A.min、最大邊為A.max，而Box B同理。

如上圖所示，當A.max < B.min時，代表兩物體之間仍有縫隙，沒有發生碰撞。

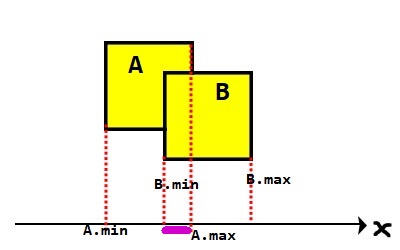
上圖可以明顯地看到A與B發生碰撞，當A.max > B.min時，代表兩物體之間沒有縫隙，發生碰撞。

但前面只討論B在A右側，當B在A的左側時，條件就要稍微改一下，

當B在A的左側時，B.max > A.min時發生碰撞。

 

將兩張圖的結果合在一起，整理成code:

1
2
if (A.max > B.min && B.max > A.min)
    Console.log("Collided");

為什麼使用 AND 來判斷?

只要A在B的右邊，那麼A.max就會永遠大於B.min，因為A.max > B.min是用在A在左邊的碰撞判斷，所以只要沒有發生碰撞，就代表只有一個條件會是True，碰撞無法成立，所以使用 AND。

 

那麼當A在B的上面或下面呢?

方法是一樣，對Y軸上的min、max判斷即可。

 

讓我們來看看程式碼 :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
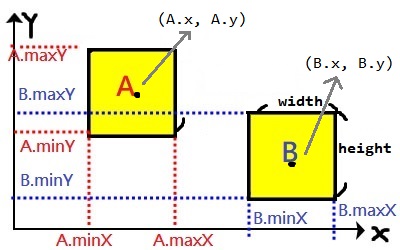
function RectCollision(r1, r2) {
    // 這邊因為(X,Y)在方塊中心
    // 所以在取得min、max時，要 +/- width/2
    // Rect1
    var minX1 = r1.x - r1.width / 2,
        maxX1 = r1.x + r1.width / 2,
        minY1 = r1.y - r1.height / 2,
        maxY1 = r1.y + r1.height / 2;
    // Rect2
    var minX2 = r2.x - r2.width / 2,
        maxX2 = r2.x + r2.width / 2,
        minY2 = r2.y - r2.height / 2,
        maxY2 = r2.y + r2.height / 2;
 
    if (maxX1 > minX2 && maxX2 > minX1 &&
        maxY1 > minY2 && maxY2 > minY1) {
        return true;
    }
    else
        return false;
}

測試結果:

原始碼在結尾與感想的最後。

 

 

如上圖，我們能明顯的看出兩物體沒有發生碰撞，但是用AABB碰撞檢測，答案卻是…發生碰撞。

 

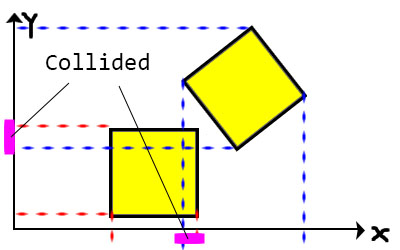
AABB碰撞檢測算法雖然計算方法簡單、速度快，但卻有幾個問題:

1.當物體旋轉時就無法檢查

2.只能檢查矩型物體

 

那麼要如何解決這兩個問題呢?

沒錯，就是本文的主題「SAT碰撞檢測」，這個方法可以完美的解決這兩個問題。

 

讓我們進入下一階段。

 

2. 什麼是分離軸檢測?

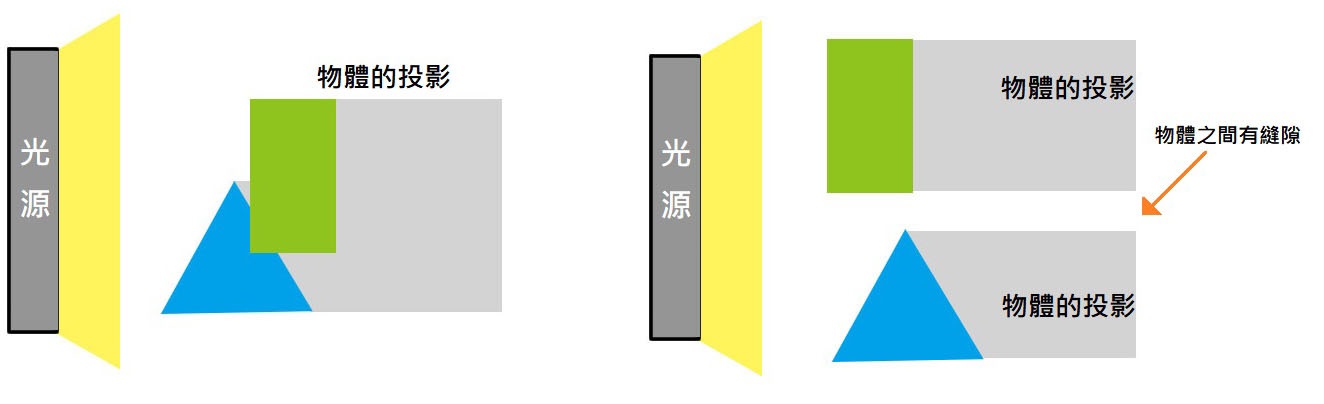
如果有兩個凸多邊形，在任意角度下的投影皆有重疊，代表物體發生碰撞，否則只要有縫隙，就代表沒有碰撞。

這張圖看不清楚的話，建議右鍵->在新分頁中開啟圖片

簡單來說，就是如果能在兩個物體間找到一條線來分離它們，那麼就代表這兩個物體之間沒有發生碰撞。

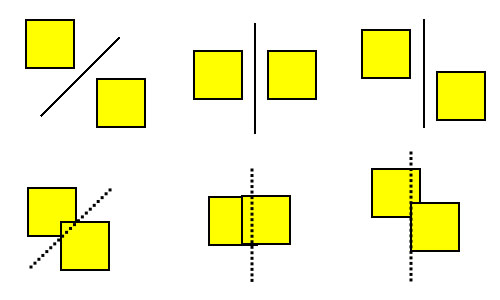
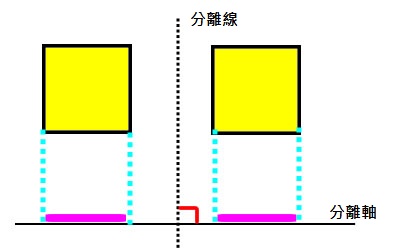
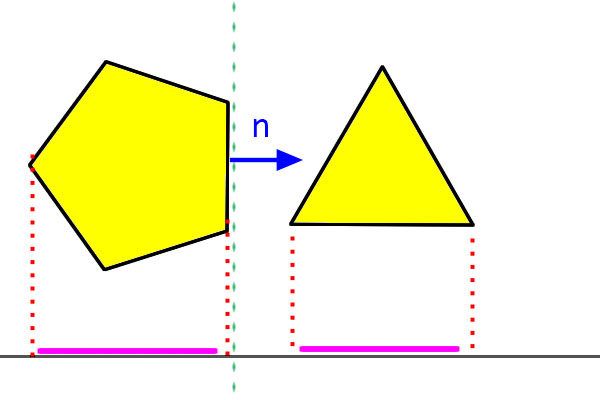
上圖中你可以看到第一排的物體之間有縫隙，所以能夠輕鬆地畫出一條線來分離它們，但第二排就沒辦法，因為這兩個物體已經相撞，之間沒有縫隙，所以找不出一條線來當分離線。

而分離線不只一條 :

到目前為止你已經大概了解什麼是分離線，聰明的你一定了解如何利用分離線來做碰撞檢測了。很簡單，只要檢查兩物體之間能不能找到分離線即可，因為只要找到一條分離線就代表物體之間有縫隙，表示沒有發生碰撞。

 

而所謂的分離軸就是與分離線垂直的一條線，透過分離軸上物體的投影，來判斷是否發生碰撞。

 

所以我們能透過分離軸檢查旋轉的物體。

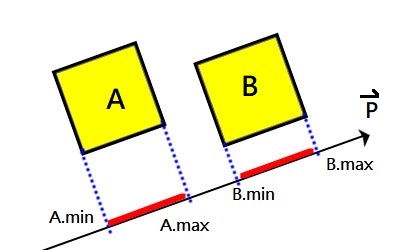
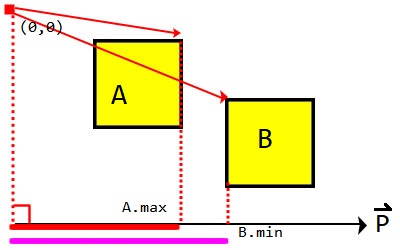
假設向量P是45度的延長線，由上圖可知，如果我們將A、B的「四個角投影在P向量上」，可以得到它們的min、max，接下來就能透過min、max來判斷碰撞。

 

這時因該會有幾個問題:

  1. 如何取得分離軸上的投影?
  2. 如何取得分離軸?

 

但是在解決那兩個問題前，先來看看前面這段話「四個角投影在P向量上」:

  1. 要如何計算其中一個角落在P向量上的投影?
  2. 要如何取得旋轉後的4個角?

 

所以在前往下一個階段之前，要先補充一些數學的知識。

 

 

3. 知識補充1 – 向量

知識補充1與2這兩段，可以先跳過，不影響閱讀，等到有看不懂的地方再回來看也行

 

為了解釋如何取得投影與分離軸，所以需要先補充向量的知識。

 

如果你的數學向量忘光的話，這裡推薦幾部教學影片:

南投高中數學課:
向量內積公式說明
單位向量的說明

Q仔高中數學教室:
向量的內積
向量內積的幾何意義與座標表示法

向量的內積:

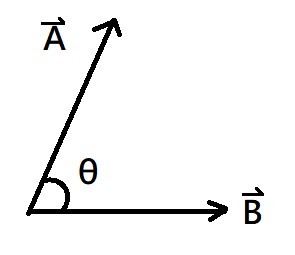
我們可以透過兩向量之間的夾角來計算點積:

\(\vec A \cdot \vec B = \left | A \right |\left | B \right | \cos \theta\)

或使用座標來計算:

\(\vec A \cdot \vec B =A_{x} B_{x} + A_{y}B_{y}\)

有了這兩個公式後，就可以開始來證明文章需要的公式了

 

 

正射影:

\(\vec A \cdot \vec B = \left | \vec A \right |\left | \vec B \right | \cos \theta \)

 

\(\cos \theta = \frac{\vec A \cdot \vec B}{\left | \vec A \right |\left | \vec B \right |} =\frac{\left | \vec P \right |}{\left | \vec A \right |}\)

然後我們就會得到向量P的長度

\(\left | \vec P \right | =\frac{ \left | \vec A \right | (\vec A \cdot \vec B)}{\left | \vec A \right |\left | \vec B \right |}=\frac{ \vec A \cdot \vec B}{\left | \vec B \right |}\)

但這裡求出的P是長度(正射影長)，只有大小，沒有方向

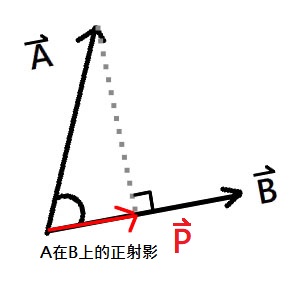
回到上圖可以觀察出P向量的方向是延著B向量，所以只要讓 純量P * 單位向量B，就能得到A在B上的正射影。

\(\vec P=\frac{ \vec A \cdot \vec B}{\left | \vec B \right |} * \frac{\vec B}{\left | \vec B \right |} =\frac{(\vec A \cdot \vec B)\vec B}{\left | \vec B \right |^{2}}\)

所謂的單位向量就是大小為1的方向向量，而純量只有大小，兩個相乘即可得到長度為P且方向為B的向量 (如果還是不太懂的話可以自己畫圖證明看看)。

所以正射影是A向量在B向量上的分量。

了解正射影後，就能取得物體在分離軸上的投影了。

 

 

法向量:

定義:垂直於平面的向量。

\(\vec A \cdot \vec B =A_{x} B_{x} + A_{y}B_{y}\)

從點積公式可以得出，當兩向量垂直時，向量內積會是零。

 

假設A向量為(3, 4)，求A的法向量，那麼我們只要將A帶進去，並湊一個能滿足等式為零的參數就是法向量。

\((3)(B_{x}) + (4)(B_{y}) = 0\)

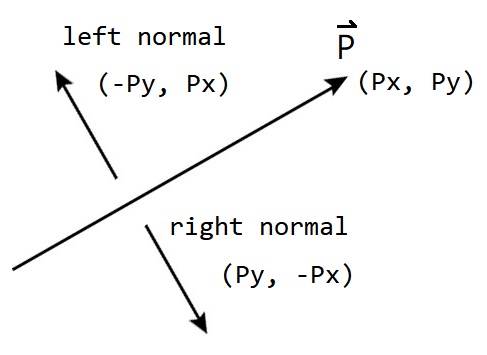
這時B向量會有無限多組合，但是有其中兩組(4, -3)、(-4, 3)，剛好就是A向量的座標互換並加負號。

 

所以我們可以得到下圖結果:

了解如何取得法向量後，就能取得需要檢查的分離軸了。

 

 

有了向量、內積、正射影長、法向量，讓我們建立一個簡易的向量函式庫吧

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
function Vector(x, y) {
    this.x = x;
    this.y = y;
}
// 取得這個自己的長度
Vector.prototype.length = function () {
    return Math.sqrt(this.x * this.x + this.y * this.y);
}
// 取得自己與vec2的內積
Vector.prototype.dot = function (vec2) {
    return this.x * vec2.x + this.y * vec2.y;
}
// 取得自己在vec2上的正射影長
Vector.prototype.projectLengthOnto = function (vec2) {
    var dotProduct = this.dot(vec2);
    var len = vec2.length();
    return dotProduct / len;
}
// 取得自己的左法向量
Vector.prototype.normalL = function () {
    return new Vector(-this.y, this.x);
}
// 取得自己的右法向量
Vector.prototype.normalR = function () {
    return new Vector(this.y, -this.x);
}

使用方式:

1
2
3
4
5
6
7
var vec1 = new Vector(3, 4);// 建立vec1向量
var vec2 = new Vector(1, 0);// 建立vec2向量
vec1.length() // => 5
vec1.dot(vec2) // => 3
vec1.projectLengthOnto(vec2) // =>3
vec1.normalL() // = (-4, 3)
vec1.normalR() // = (4, -3)

 

 

4. 知識補充2 – 旋轉變換

為了解釋如何取得物體旋轉後的角落，所以需要先補充旋轉變換的知識。

 

其作用為以原點為中心旋轉θ角:

說明:

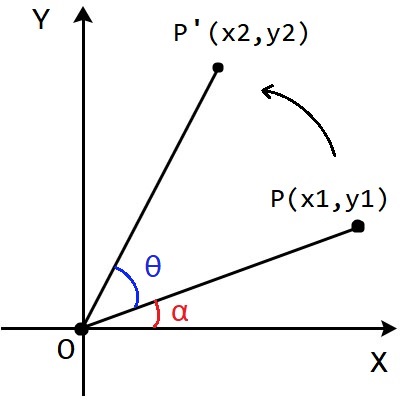
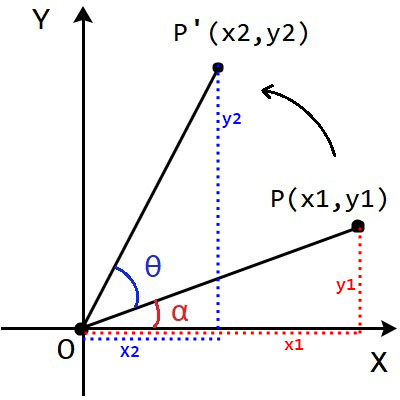
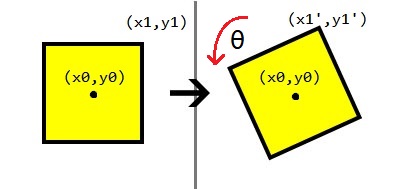
如上圖，座標平面上\(L = \overline{OP}\)

且點\(P(x_{1}, y_{1})\)滿足\(x_{1} = L*\cos \alpha, y_{1} = L*\sin \alpha\)

那麼，以原點O為中心，將這個點以逆時針旋轉 \(\theta\)角後得到\(P'(x_{2}, y_{2})\)

 

方法一:

先取得\(\overline{OP}\)與\(\alpha\)，那麼\(P’\)就是\(( L*\cos (\alpha +\theta ), L*\sin (\alpha +\theta ) )\)

 

但在電腦中取得OP長要透過畢氏定理開根號來取得，加上只有P點不知道α角的時候，要再叫用Math.atan2(y, x)取得α後在計算，比較麻煩。

所以有一個改良版

和角公式:

\(\begin{cases} \cos(\alpha+\theta ) = \cos \alpha \cos \theta – \sin \alpha \sin \theta \\ \sin(\alpha+\theta ) = \sin \alpha\cos \theta + \cos \alpha\sin \theta \end{cases}\)

所以

\(\begin{cases} \cos(\alpha+\theta ) = \frac{x_{2}}{L} = \frac{x_{1}}{L}\times \cos\theta – \frac{y_{1}}{L} \times \sin\theta \\ \sin(\alpha+\theta ) = \frac{y_{2}}{L} = \frac{y_{1}}{L}\times \cos\theta – \frac{x_{1}}{L} \times \sin\theta \end{cases}\)

同乘L後即可得到

\(\begin{cases} x_{2}=x_{1}\cos \theta-y_{1} \sin\theta \\ y_{2}=y_{1}\cos\theta+x_{1}\sin\theta \end{cases}\)

而這個就是我們要的旋轉公式

 

矩陣表示法

\(\left[ {\begin{array}{*{20}{c}} {x_{2}}\\ {y_{2}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ – \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} x_{1}\\ y_{1} \end{array}} \right]\)

而下面這矩陣就是所謂的旋轉矩陣，未來電腦圖學會很常用到

\(\left[ {\begin{array}{*{20}{c}} {\cos \theta }&{ – \sin \theta }\\ {\sin \theta }&{\cos \theta } \end{array}} \right]\)

 

講解完後，讓我們把這段公式加入我們的向量函式庫吧。

angle為弧度，並以原點(0,0)為中心旋轉angle角:

1
2
3
4
5
6
7
Vector.prototype.rotate = function (angle) {
    var new_x = (this.x * Math.cos(angle)) - (this.y * Math.sin(angle));
    var new_y = (this.x * Math.sin(angle)) + (this.y * Math.cos(angle));
 
    this.x = new_x;
    this.y = new_y;
}

 

5. 如何取得分離軸上的投影?

有了投影公式後，接下來只要把A、B的四個角投影在P向量上就能知道min、max了。

 

這時卻出現了一個狀況，如果兩個物體方向不一樣呢?

由上圖可知，當兩物體方向不同時，只要在4個角落中選一個最小和最大的，就是min、max。

 

那我們要如何透過投影來判斷碰撞?

由上圖可以看到，A.max、B.min在P向量上的投影圖。

當B.min > A.max時，代表他們之間有分離線，所以沒有碰撞。當位置交換時，A.min > B.max時代表有間距。

 

讓我們把結果整理成code

1
2
3
4
if (B.min > A.max || A.min > B.max)
    Console.log("分離");// isSeparated
else
    Console.log("碰撞");// isCollided

這邊選擇True為分離是因為這是分離軸檢測，我認為這樣比較符合。

 

了解如何取得min、max，並如何判斷後，就可以進入下個階段了。

 

 

6. 編寫程式碼-投影、旋轉與判斷

第一步，我們需要取得矩形上的四個角，這時就需要前面的「知識補充2-旋轉變換」

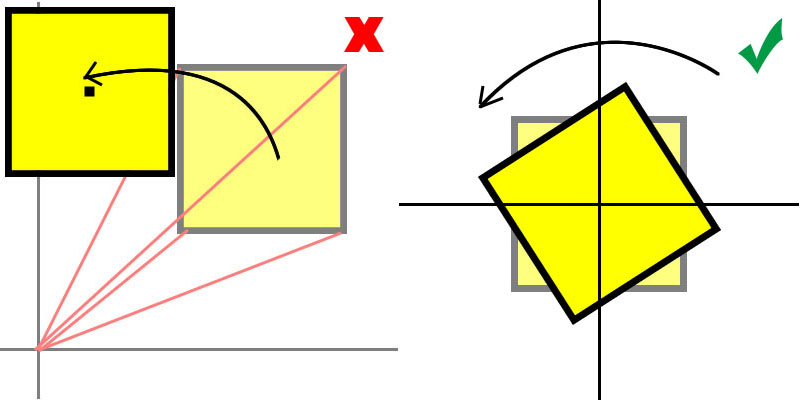
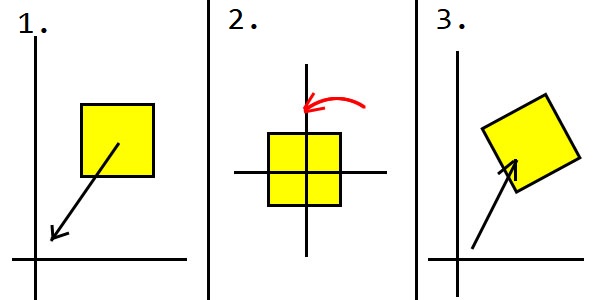
如果直接將四個角套用旋轉公式的話，就會像左圖一樣，物體繞中心旋轉。

但我們想要的是右圖中，物體原地旋轉的效果，所以要將旋轉公式做點更動。

如上圖的步驟，我們需要的旋轉是以矩形中心為參考點做旋轉，而原公式以原點做旋轉，所以需要先將物體平移到原點，旋轉完後再將其平移回來。

\(\left\{\begin{matrix}x_{1}’ = [(x_{1}-x_{0})\cos\theta-(y_{1}-y_{0})\sin\theta] + x_{0}\\ y_{1}’ = [(y_{1}-y_{0})\cos\theta+(x_{1}-x_{0})\sin\theta] + y_{0}\end{matrix}\right.\)
讓我們把這個公式加入向量函式庫

1
2
3
4
5
6
7
8
// angle:弧度, refP:參考點
// 作用: 以refP為參考點，旋轉angle角
Vector.prototype.rotateRefPoint = function (angle, refP) {
    let new_x = (this.x - refP.x) * Math.cos(angle) - (this.y - refP.y) * Math.sin(angle) + refP.x;
    let new_y = (this.y - refP.y) * Math.cos(angle) + (this.x - refP.x) * Math.sin(angle) + refP.y;
    this.x = new_x;
    this.y = new_y;
}

 

 

然後讓我們來建立一個基本的物體:

先簡單寫出Box的結構

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
function Box(x, y, w, h) {
    this.pos = new Vector(x, y);// 中心
    this.w = w;
    this.h = h;
    // 以順時針紀錄矩形的四個角
    this.corners = [
        new Vector(w / 2, -h / 2),
        new Vector(w / 2, h / 2),
        new Vector(-w / 2, h / 2),
        new Vector(-w / 2, -h / 2)
    ];
    // 假設角度是45
    this.directionAngle = toRadio(45);// 將45換成弧度
 
    this.getVertices = function () {
        var vertices = [];
        // 順時針走訪角落
        for (var i = 0; i < this.corners.length; i++) {
            var p1 = this.corners[i];
 
            var vec = new Vector(this.pos.x + p1.x, this.pos.y + p1.y);
            // 將各個角以物體中心為參考點來旋轉
            vec.rotateRefPoint(this.directionAngle, this.pos);
 
            vertices.push(vec);
        }
        // 最後回傳以物體中心為參考點選轉後的角落
        return vertices;
    }
}

接下來只要呼叫getVertices()就能取得四個角的陣列了

1
2
// 取得box1的4個角
var boxA_Vertices = boxA.getVertices();

 

第二步，取得box1在分離軸上的min、max投影。而box2也是一樣的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/ 假設分離軸為45度角
var axis = new Vector(1, -1);
 
// 取得box1的4個角
var boxA_Vertices = box1.getVertices();
 
// 先以第一個角當初始值
// vec.projectLengthOnto(axis) : 取得vec在axis上的投影長
var min_proj_boxA = boxA_Vertices[0].projectLengthOnto(axis);
var min_index_boxA = 0;
 
var max_proj_boxA = boxA_Vertices[0].projectLengthOnto(axis);
var max_index_boxA = 0;
 
// 再從剩下的3個角選出最大和最小投影
for (var i = 1; i < 4; i++) {
    var current = boxA_Vertices[i].projectLengthOnto(axis);
 
    // 選擇最小投影
    if (current < min) {
        min_proj_boxA = current;
        min_index_boxA = i;
    }
    // 選擇最大投影
    if (current > max) {
        max_proj_boxA = current;
        max_index_boxA = i;
    }
}

 

最後，當我們有了box1和box2的min、max後，就可以檢查他們是否在axis這個軸上碰撞

1
2
3
4
if (min_proj_boxB > max_proj_boxA || min_proj_boxA > max_proj_boxB)
    Console.log("分離");// isSeparated
else
    Console.log("碰撞");// isCollided

 

讓我們把min、max的取得整理一下，變成可呼叫的方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
// getMinMax(頂點陣列,分離軸)
function getMinMax(vertices, axis) {
    // 先以第一個角落投影為標準
    var min_DotProduct = vertices[0].projectLengthOnto(axis),
        max_DotProduct = vertices[0].projectLengthOnto(axis);
 
    for (var i = 1; i < vertices.length; i++) {
        // 取得當前要比對的投影長度
        var temp = vertices[i].projectLengthOnto(axis);
        // 如果比當前最小的更小，紀錄它
        if (temp < min_DotProduct) {
            min_DotProduct = temp;
            min_index = i;
        }
        // 如果比當前最小的更大，紀錄它
        if (temp > max_DotProduct) {
            max_DotProduct = temp;
            max_index = i;
        }
    }
 
    var result = {
        min: min_DotProduct,
        max: max_DotProduct
    };
    // 最後傳回一個物件包含min、max屬性
    return result;
}

 

 

 

7. 如何取得分離軸?

在SAT介紹的時候也提到，兩物體間有無限多條分離軸，難不成要真的從0度~360度的分離軸全部投影一變嗎?

其實不需要，我們只需要沿著物體所有邊上的法向量當作分離軸作檢查，即可判斷。

由上圖可知，如果我們將三角形向左平移，直到與五角形投影重疊時，代表他們發生碰撞。

而綠色那條分離線，可以當作五角形守備的領域，只要有東西進到這裡，就代表碰撞。

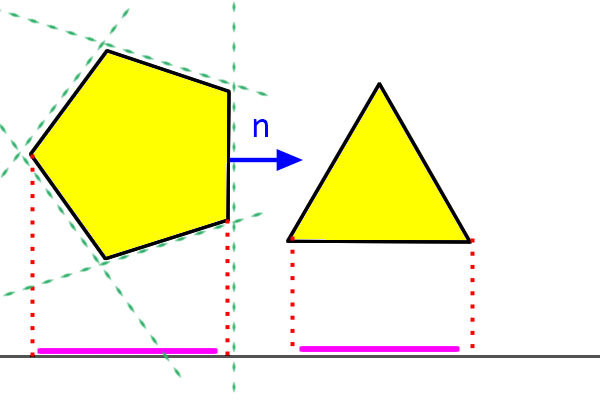
如上圖，將五角形每個邊上的檢查線都畫出來後，只要取跟檢查線垂直的軸，就是我們需要的分離軸。

只要有任何物體進入綠色分離線的包圍區，就代表物體與五角形發生碰撞。

 

那麼要如何取得邊上的法向量?

這時候就是補充知識1-法向量派上用場的時候了。

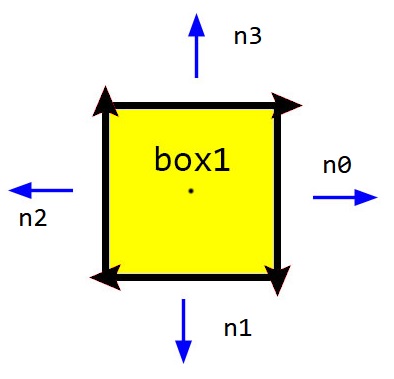
如上圖，對每個邊向量取法向量即可，而我這邊以順時針、取左法向量為例子。

可以發現，在矩形中會有兩組方向相反的法向量，所以可以透過優化找出重複的法向量增加效率，但通常只對矩形有效果。

 

先讓讓我們在Box物件中再加入getNorms()這個方法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
function Box(x, y, w, h) {
    // ...省略...
    this.getNorms = function () {        
        var vertices = this.getVertices();// 取得頂點
        var norms = [];
        var p1, p2, n;
 
        // 順時鐘
        for (let i = 1; i < vertices.length; i++) {
            p1 = vertices[i - 1];
            p2 = vertices[i];
            // 取得這個邊的左法向量
            n = new Vector(p2.x - p1.x, p2.y - p1.y).normalL();
            // 加入這個法向量
            norms.push(n);
        }
        // 補上最後一個邊
        p1 = vertices[vertices.length - 1];
        p2 = vertices[0];
        n = new Vector(p2.x - p1.x, p2.y - p1.y).normalL();
        norms.push(n);
        // 最後傳回這個物體所有邊上的左法向量
        return norms;
    }
}

有了頂點取得的方式、投影大小的判斷加上邊上法向量的取得，我相信你已經有足夠的知識來完成SAT碰撞檢測了。

 

 

8. 粗糙的矩形檢測

讓我們來看看針對矩形的程式碼，這段程式碼單純是了解檢查過程，如果你對判斷的方法不是很清楚的話希望你花一些時間看一下，後面會在寫出一個整理過的寫法。

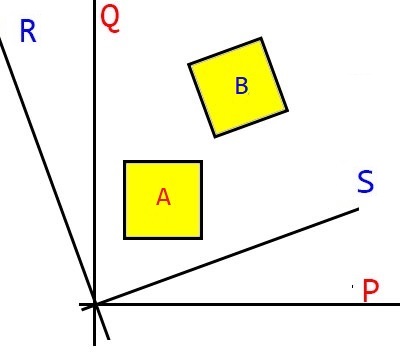
這裡我假設A方塊的法向量是P、Q，B方塊的法向量是S、R，手動對它們一一檢查

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
function SAT_Collision(boxA, boxB) {
    var vertices_boxA = boxA.getVertices();
    var vertices_boxB = boxB.getVertices();
    var norms_boxA = boxA.getNorm();
    var norms_boxB = boxB.getNorm();
 
    // 假設boxA的法向量為P、Q，boxB為R、S
    // boxA、boxB在P、Q檢查軸上的投影
    var MinMax_PA = getMinMax(vertices_boxA, norms_boxA[0]);
    var MinMax_PB = getMinMax(vertices_boxB, norms_boxA[0]);
    var MinMax_QA = getMinMax(vertices_boxA, norms_boxA[1]);
    var MinMax_QB = getMinMax(vertices_boxB, norms_boxA[1]);
    // boxA、boxB在R、S檢查軸上的投影
    var MinMax_RA = getMinMax(vertices_boxA, norms_boxB[0]);
    var MinMax_RB = getMinMax(vertices_boxB, norms_boxB[0]);
    var MinMax_SA = getMinMax(vertices_boxA, norms_boxB[1]);
    var MinMax_SB = getMinMax(vertices_boxB, norms_boxB[1]);
    
    // 在分離軸上是否分離
    var separate_P = MinMax_PB.min_proj > MinMax_PA.max_proj ||
                     MinMax_PA.min_proj > MinMax_PB.max_proj;
    var separate_Q = MinMax_QB.min_proj > MinMax_QA.max_proj ||
                     MinMax_QA.min_proj > MinMax_QB.max_proj;
    var separate_R = MinMax_RB.min_proj > MinMax_RA.max_proj ||
                     MinMax_RA.min_proj > MinMax_RB.max_proj;
    var separate_S = MinMax_SB.min_proj > MinMax_SA.max_proj ||
                     MinMax_SA.min_proj > MinMax_SB.max_proj;
 
    var isSeparated = separate_P || separate_Q || separate_R || separate_S;
    if(isSeparated)
        Console.log("分離");// isSeparated
    else
        Console.log("碰撞");// isCollided
}

測試結果:

但上面那個只適用在矩形上，而且Code又醜又長，所以讓我們把它整理一下。

 

 

9. 編寫程式碼 – 多邊形與多邊形

雖然這裡的寫法也還是沒有完全優化，其實你可以將normal_polygonA、B合併後在一起走訪，但我想範例這樣比較容易了解。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
// true:兩物體分離, false:兩物體碰撞
function SAT_Collision(polygonA, polygonB) {
    // 取得多邊形每個邊上的法向量，回傳陣列
    var normal_polygonA = polygonA.getNorm(),
        normal_polygonB = polygonB.getNorm();
    // 取得多邊形的頂點陣列，回傳陣列
    var vertices_polygonA = polygonA.getVertices(),
        vertices_polygonB = polygonB.getVertices();
 
    var isSeparated = false;
 
    // 透過迴圈走訪多邊形A的法向量，來檢查是否分離
    for (var i = 0; i < normal_polygonA.length; i++) {
        var minMax_A = getMinMax(vertices_polygonA, normal_polygonA[i]);
        var minMax_B = getMinMax(vertices_polygonB, normal_polygonA[i]);
 
        isSeparated = (minMax_B.min > minMax_A.max || minMax_A.min > minMax_B.max);
        // 只要發現有一條分離線，就代表物體沒有發生碰撞
        if (isSeparated) return true;
    }
 
    // 透過迴圈走訪多邊形B的法向量，來檢查是否分離
    for (let i = 0; i < normal_polygonB.length; i++) {
        var minMax_A = getMinMax(vertices_polygonA, normal_polygonB[i]);
        var minMax_B = getMinMax(vertices_polygonB, normal_polygonB[i]);
 
        isSeparated = (minMax_B.min > minMax_A.max || minMax_A.min > minMax_B.max);
        if (isSeparated) return true;
    }
    // 如果所有法向量都檢查過後，沒有發現分離，代表兩物體碰撞
    return false;
}

由Code可以看到，只要物體間有分離，就可以跳出並回傳結果，不需要再去檢查B的法向量。

要注意這邊的isSeparated在分離時為Ture、碰撞時為False，如果你要以碰撞作檢查的話記得加上NOT。

 

使用範例:

1
2
3
4
5
6
7
8
9
function update(dt) {
    polygonA.update(dt);
    polygonB.update(dt);
 
    var isCollided = !SAT_Collision(polygonA, polygonB);
    if(isCollided){
        // ...發生碰撞後要做的事...
    }
}

測試結果:


原始碼在結尾與感想的最後。

 

 

10. 編寫程式碼 – 多邊形與圓

其實多邊形與圓的測試是一樣的，先看看這張圖:

聰明的你看到這張圖，大概就能明白我想說什麼了。

在做圓的判斷時，因為圓心到各個點長度都是R，所以我們可以透過圓心的投影來 +/- Radius來得到min、max

Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
function SAT_CircleToPolygon(circle, polygon) {
    var normal_polygon = polygon.getNorm();
    var vertices_polygon = polygonA.getVertices();
    
    var center = circle.pos;
    var radius = circle.radius;
 
    var isSeparated = false;
 
    for (var i = 0; i < normal_polygon.length; i++) {
        var minMax_P = getMinMax(vertices_polygon, normal_polygon[i]);
        // 計算圓的min、max
        var projectLen_C = center.projectLengthOnto(normal_polygon[i]);
        var min_C = projectLen_C - radius;
        var max_C = projectLen_C + radius;        
 
        isSeparated = (min_C > minMax_P.max || minMax_P.min > max_C);
        // 只要發現有一條分離線，就代表物體沒有發生碰撞
        if (isSeparated) return true;
    }
    return false;
}

測試範例(因為我沒有自己實作，所以這個動畫引用自這裡，雖然我的做法跟他的不太一樣，不過結果是一樣的):

 

 

11. SAT的總結

關於SAT的優缺點:

  1. SAT的方法是些假設兩物體是分離的，並在檢查中只要成功找到正確的分離軸，就直接跳出，所以當物體都是分離狀態時，SAT的效率是非常高的。
  2. 只要物體之間有碰撞，SAT就必須檢查所有的法向量，來確保物體之間沒有分離線，越多的物體發生碰撞，效率也就越低。
  3. 因為SAT是採用所有法向量來作檢測，當多邊形的邊越多時，效率也會越來越低，但可以透過找出正負相反的法向量來減少檢查次數。
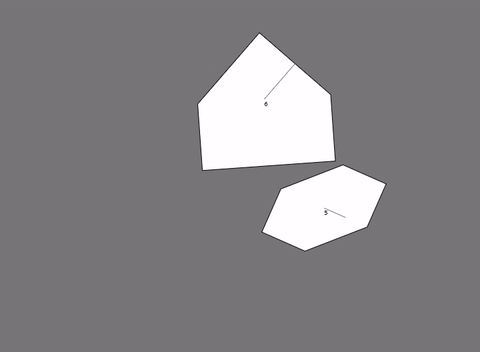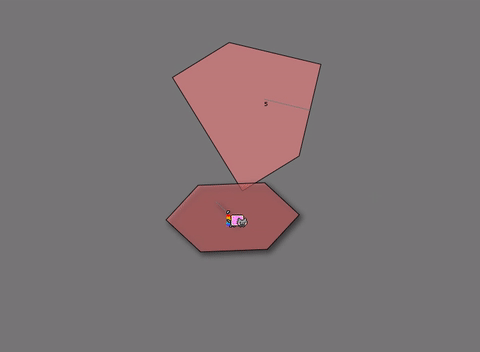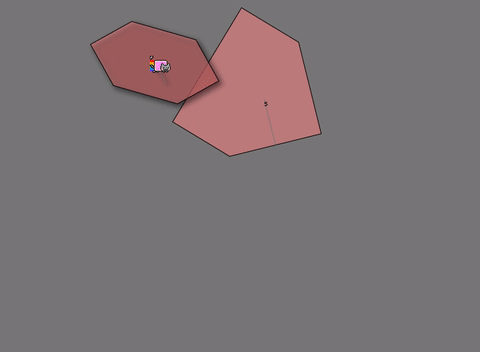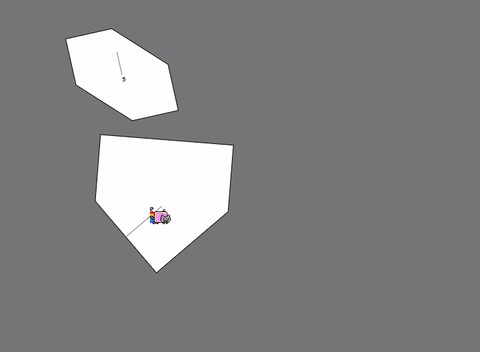
  4. SAT雖然無法檢查凹多邊形，但是能透過將多個凸多邊形組合成凹多邊形的形狀，來作碰撞檢測。

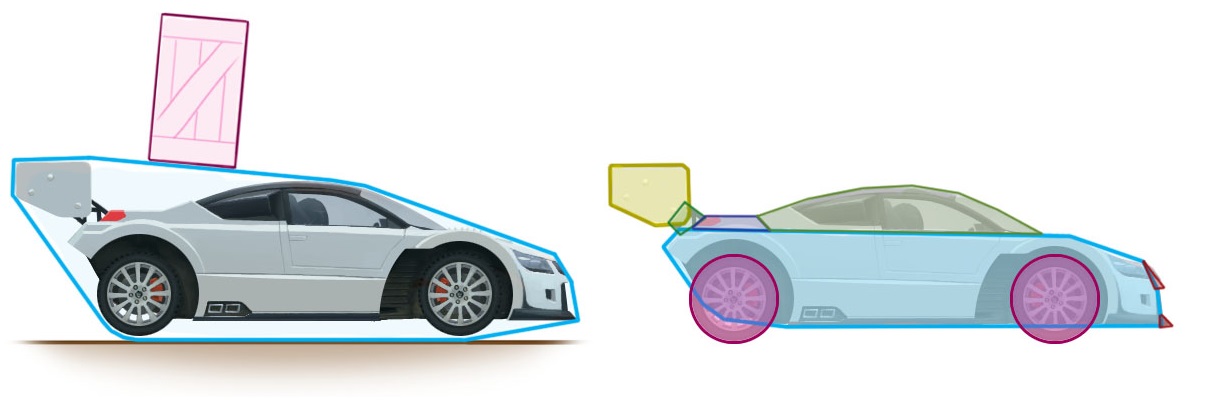
如上圖中的賽車，雖然它的形狀是凹邊形，但能透果右邊的方式來做精密的碰撞檢測

5. SAT在運算時能夠取得碰撞物體間的最小穿透量(MTV, Minimum translation vector)，所以能夠處理物體間的碰撞回饋，並進一步地達成剛體動力學的模擬。

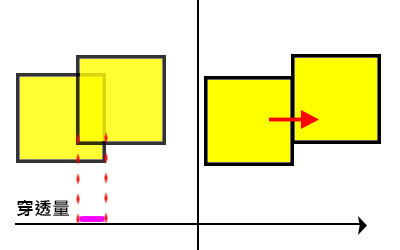
如上圖，當我們希望物體不要發生穿透時，就會需要所謂的MTV，當物體穿透時，選一個最小的穿透量，將它平移回去

 

所以SAT碰撞在做過效能調整後，是很好的碰撞檢測演算法，靈活度也很高，是很多物理引擎會採用的檢測法之一。

還有另一個凸邊形的高效演算法GJK以疊代地生成單形以對兩個凸集求閔可夫斯基和，有興趣可以研究看看。

 

如果對碰撞方法有興趣的話可以參考這篇:

Bullet physics engin軟體工程師-Erwin Coumans: Collision Detection for Real-Time Simulation

其他相關資源:

SAT (Separating Axis Theorem)

2D Collision Detection

2D polygon-based collision detection and response

Video Game Physics Tutorial

 

 

12. 多物體的碰撞優化

當我們要檢查多個物體碰撞時，通常會直接對所有物體互相進行判斷，就像下面這段Code:

基本枚舉法的Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function update(dt) {
    // ...更新物體狀態...
    for (var i = 0; i < shapes.length; i++) {
        for (var j = 0; j < shapes.length; j++) {
// 如果是同個物體就跳過
            if (i == j) continue;
 
            var isCollided = !SAT_Collision(shapes[i], shapes[j]);
            if(isCollided){
                // ...碰撞事件...
            }            
        }
    }    
}

shapes是指所有的物體陣列

 

用這種最直觀的方式檢查，時間複雜度會達到O(n!)，當場景複雜，需要檢測的物體變多後，用枚舉的方式檢測可能會導致遊戲延遲。

其中最大的問題就是，當場景中有兩個距離非常遠的物體，遠到根本不可能發生碰撞，卻照樣對他們進行檢測，導致效能的浪費。

 

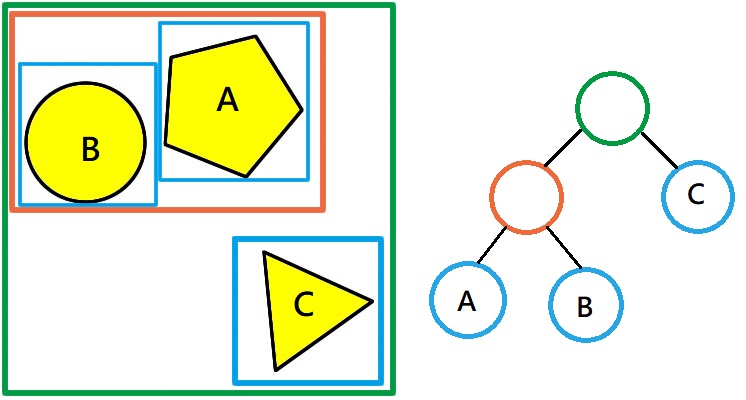
這裡簡單的介紹一個優化方法 – AABB Tree:

建立ABT的方法跟建立二元樹的方法一樣，來看執行步驟:

  • Step1. 把A加入樹中，作為根結點。
  • Step2. 把B加入樹中，判斷是否與根結點A有碰撞，如果有的話就在繼續比較子節點，如果都沒有與子節點有碰撞，就把B加入子節點後，如果與節點都沒有碰撞的話，就把A、B當作一個新區域，並生成A、B的父節點(橘色圈圈)。
  • Step3. 把C加入樹中，方法跟Step2一樣，最後得到上圖中的樹。

假如我要檢查A物體時，只需要檢查同在橘色區域的B物體即可。

 

AABB Tree在建立時，就先把有機會碰撞的放在同一區，有了這樣的結構後，要判斷碰撞的效率就提高了，因為只需判斷與該物體同區域的物體即可，並不需要全部檢查，使得時間複雜度縮減到O(log n)。

 

而其他多物體碰撞的演算法還有:

四叉樹(Quad Trees)、八叉樹(octree)、二元分割樹(BSP tree)、kd樹、球體樹(sphere tree)、R樹(R tree)、碰撞投影、光線投影等等…，有興趣的可以在自己研究。

 

 

13. 動態物體間的碰撞檢測

這裡為大家提供一些解決的方向，我目前知道有這種解決方法，但礙於能力不足，只研究到觀念部分。

 

在我們前面講的碰撞檢測方法都只適用在靜態，什麼意思呢?

在遊戲中做的碰撞檢測其實是以離散時間來模擬，因此在每個瞬間，物體的位置和方向是靜止的，就像快照一樣，若物體的移動速度與其相對尺寸來說不是太快的話，這種方法是可行的，事實上在許多物理引擎中，都是使用這種方法。

但對於較小且高速的移動物體，這種方法就會失效，想像現在有個很小的物體，他每次更新時的移動幅度大於碰撞體的尺寸，就會發生「穿隧」的問題。

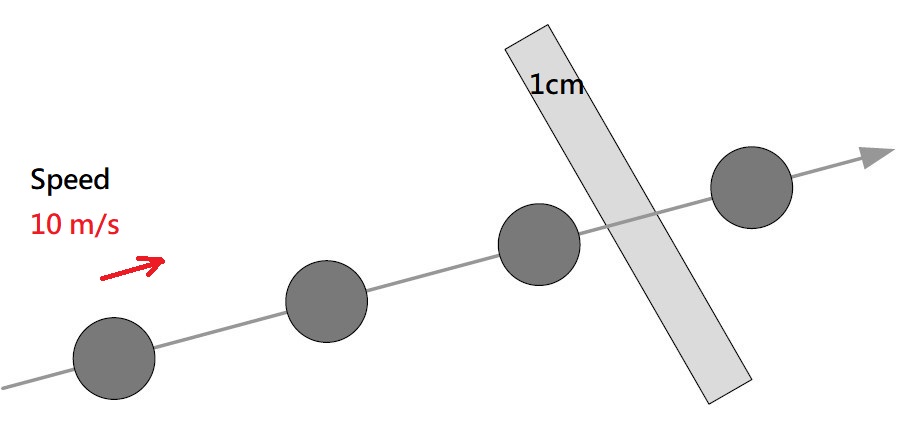
如上圖所示，細小且快速的物體移動時，其路徑可能留下縫隙，導致碰撞失效。

 

解決方法

掃描形狀(swept shape):

對一個物體的位置、速率與加速度取線性穿插，得到一個時間段的物體快照，再透過掃描的形狀做檢測。

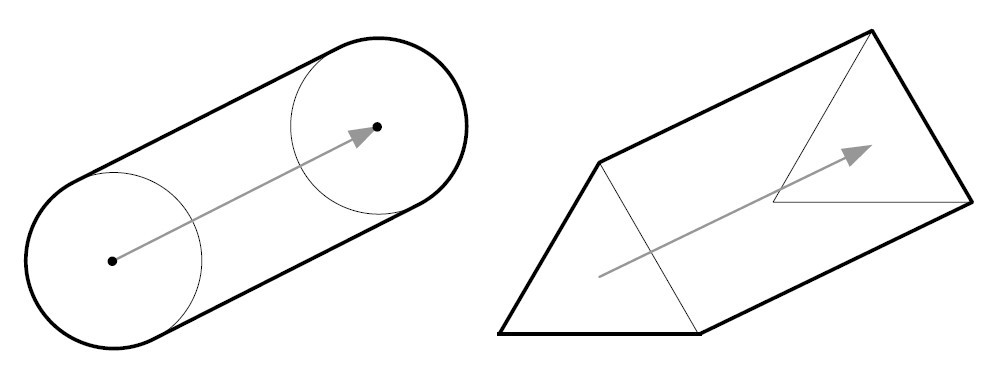
如上圖，中間的移動量就是兩次快照間的穿隧量，而球體的掃描體變成膠囊狀，三角形的掃描體變成三角柱。

 

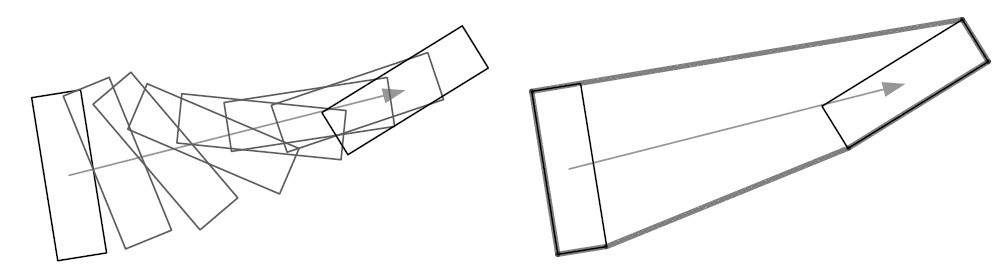
若要掃描的物體正在旋轉，也能透過線性穿插來建立掃描形狀

形狀掃描對動態物體來說，是一個有效的檢測技術，能保證不錯過快照之間的碰撞。

缺點是，若物體的行進路線為曲線甚至旋轉，僅透過線性穿插計算，其結果是不準確的，所以要再根據狀況使用更精準的技術。

 

其實還有很多更好的解決方案，有興趣的可以在自己研究。

 

 

14. 結尾與感想

那麼為什麼要對碰撞這麼刁鑽，就是為了能模擬物理效果，當碰撞的處理達到一定的程度後，就可以邁向下一個階段「剛體動力學」與「物理模擬」，讓電腦中的物體越來越接近現實，有趣吧。

光是碰撞的處理就有這麼多複雜的技術問題，就可以了解高階遊戲開發工程師是多麼厲害的一群人了。

為了做出更好的遊戲，還要很多東西要學，為了能有效的使用電腦資源，要學會作業系統架構、演算法、資料結構並精通程式語言，要能在螢幕中顯示各種效果、視角操控，還要學習電腦圖學、線性代數，為了處理物理模擬，還要學習古典物理、高等微積分，而這些東西到了三維空間後，又更加複雜，還有專案管理等等附加技能，加上遊戲工程師們也不斷的在進化，搞不好一輩子都學不完呢。

 

————————————————————————

 

終於寫完了，這篇文中我嘗試用各種插圖來解釋一些觀念，不知不覺就打了這麼多，我Coding技巧很差，範例執行的效率可能沒有很好，但我想對這篇文想表達的內容影響不大。

 

最後，感謝你的觀看，希望你在閱讀後能有些收穫。

對這文章有任何問題，歡迎在下方留言提出意見，或是E-mail與我聯絡davidmd9830415@gmail.com。

 

我的多邊形碰撞範例 : http://davidhsu666.com/downloads/Collision-SAT/ver0.2.1-polygon-merge/

自製的向量函式庫 : https://github.com/md9830415/JS-Vector2D

 

附上文章範例Source Code: https://github.com/md9830415/Collision-Detection-article

我的github中也有放多邊形碰撞的Source Code，有興趣的可以看看。

 

大概就是這樣了，讓我們下期再見，掰掰。

 

————————————————————————

 

 

參考資源 :

Game Engine Architecture, Second Edition.pdf : here

Video Game Physics Tutorial : here

Collision Detection for Real-Time Simulation : here

Collision Detection – contact generation and GPU acceleration : here

Physics – Collision in 2 dimensions : here

Collision Detection Using the Separating Axis Theorem : here

SAT (Separating Axis Theorem) : here

2D Collision Detection : here

2D polygon-based collision detection and response : here

Collision detection : here

Collision resolution : here

Introductory Guide to AABB Tree Collision Detection : here

How to Create a Custom Physics Engine : here

Vector maths – a primer for games programmers : here

平面上基本的線性變換：旋轉、鏡射、伸縮、推移 : here

二階方陣表示的線性變換 : here

AABB包围盒算法,在2D碰撞检测中的实现 : here

“等一下，我碰！”——常见的2D碰撞检测 : here

Core HTML5 Canvas: Graphics, Animation, and Game Development

7 comments

  • wen

    想請問一下

    你文內所述的二元樹如果用在隨時都在改變位置的動作or射擊遊戲內

    是要在每個loop更新時做新的二元樹排列嗎？

     

    • david

      我想是的，但就算每個Loop都重新排序，在一定的數量級，效率也比一個一個檢測來的高。

      以QuadTree為例，插入複雜度為O(n)，而搜尋複雜度大概是O(nlogn)，但原本依序檢測的複雜度是O(n*n)，就算優化過也是要全部走訪一次。

      所以我認為在一定的數量級上，會比原本的好。

  • 陳瀚志

    展維您好,

     

    最近我在寫一些碰撞程式的遊戲,無意間在google搜到你的網站.

    網站詳細說明的碰撞的一些基本概念及一些參考資源,讓我獲益匪淺.

    也在此感謝你無私的分享.

     

    現在剛好完成了初級碰撞的程式,打算開始寫動態碰撞的程式.

    發現簡單四邊形在移動過程中形成的軌跡面難以去做SAT的檢測.

    簡單來說,今天我有兩個四邊形在平面上走不同的路徑,然後用SAT去做檢測是否相撞.

    但難題是本身的路徑難以形成,就算形成後也難以做SAT的檢測.

    想請問你有在這方面有什麼高見嗎?

     

    感謝你!

    • david

      “今天我有兩個四邊形在平面上走不同的路徑,然後用SAT去做檢測是否相撞”

      我想可以先透過WASD控制矩形A，用上下左右控制矩形B，這樣測試比較方便，或是像我範例中那樣，用滑鼠拖曳來移動也行，試著找一個方法去控制物體。

  • 鄧翔宇

    你好，我在做大學作業時無意查到你的網站，內容非常詳實!
    不過，在 8. 下方的Collision detection function中的 11、12 行 應該是 norms_boxA 而非 norms_boxB

發佈留言

發佈留言必須填寫的電子郵件地址不會公開。 必填欄位標示為 *