程式隨手筆記

碰撞檢測的優化-四叉樹(Quadtree)

許多遊戲都會需要碰撞檢測來判斷兩物體的碰撞，但這些演算法通常是較為昂貴的操作，如果無法有效率的選擇檢測目標，很可能會大幅降低執行的速度。(像是之前提到的SAT碰撞檢測)

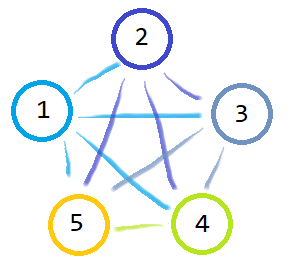
在之前的”多邊形碰撞檢測”文中，也有提到當檢測物體越來越多時，基本逐一檢測的效率會越來越差，複雜度約為O(n^2)，就算排除重複檢測過的物體，只要是逐一檢測的方法就一定會走訪所有物件。

從上圖可以得知直接全部檢測的話是4 x 5 = 20，如果扣掉重複，至少是4 + 3 + 2 + 1 = 10，但真正的問題是，就算1和3距離這麼遠，也照樣會檢查它們，那有沒有方法能解決這種狀況呢?

 

這就是文章的主要內容，QuadTree。

http://davidhsu666.com/archives/quadtree_in_2d

 

目錄

  1. 什麼是QuadTree?
  2. 插入流程
  3. 搜尋流程
  4. 實作-插入
  5. 實作-搜尋
  6. 實際應用
  7. 總結
  8. 參考資料

 

什麼是QuadTree?

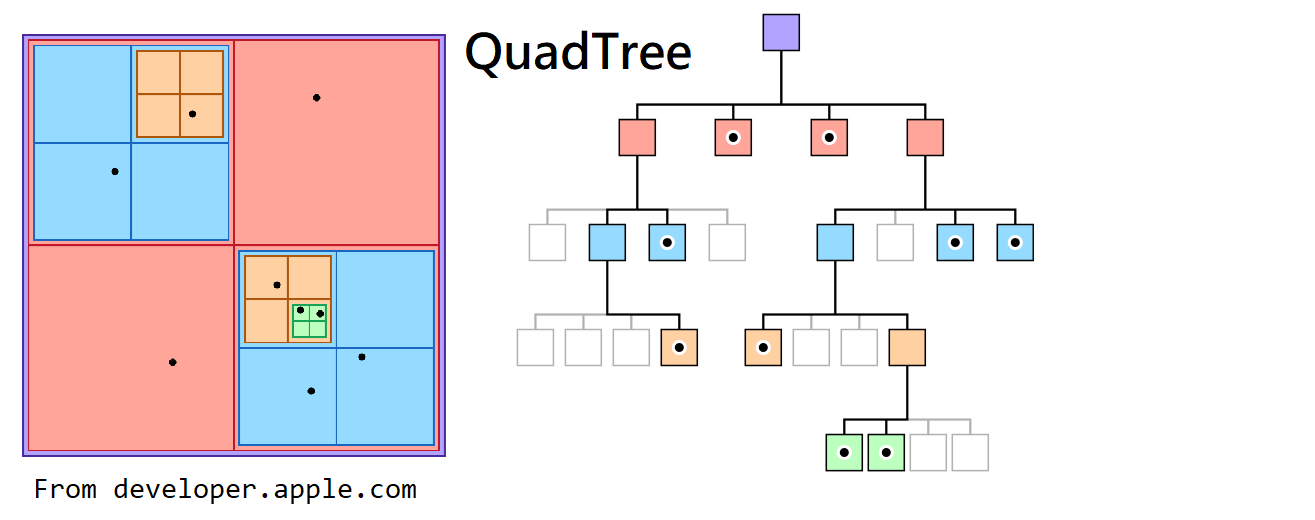
四叉樹(QuadTree)是一種劃分2D區域的樹狀資料結構，類似一般的二元樹，但子節點是4個，而不是2個。

區域的劃分架構類似這樣 :

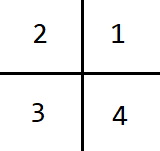
並限制每個區域能容納的上限，當超過後就將該區域再往下分割4塊，這樣就能夠將每個物體進行區域分類，這樣在檢查的時候就可以鎖定部分區域的物體，從而增加效率。

 

插入流程:

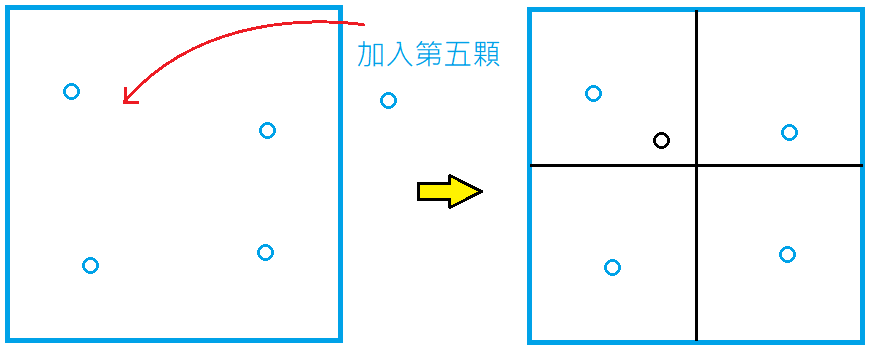
假設我先設定每個區域只能容納4個物體，只要超過該容量，就要分割該區域。

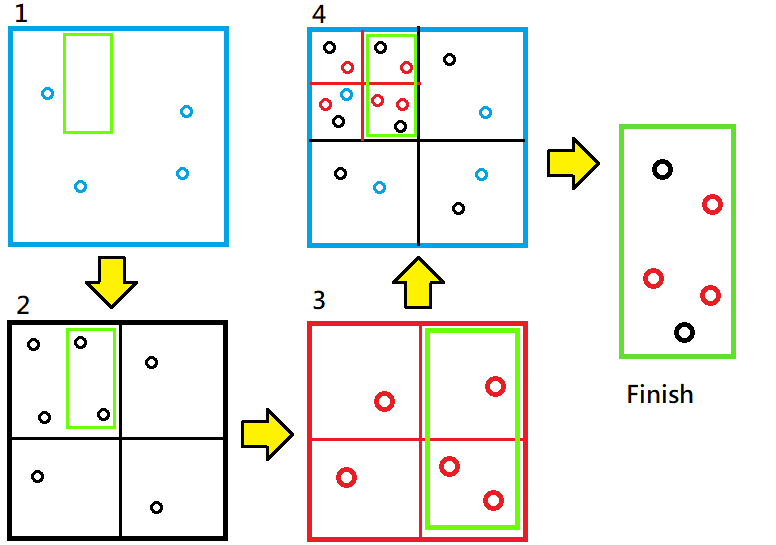
左圖方形區域已經有4個物體，想再加入第5個時，就必須分割成4個子區域，再將第5顆分類到最近的左上角區域中，如右圖:

 

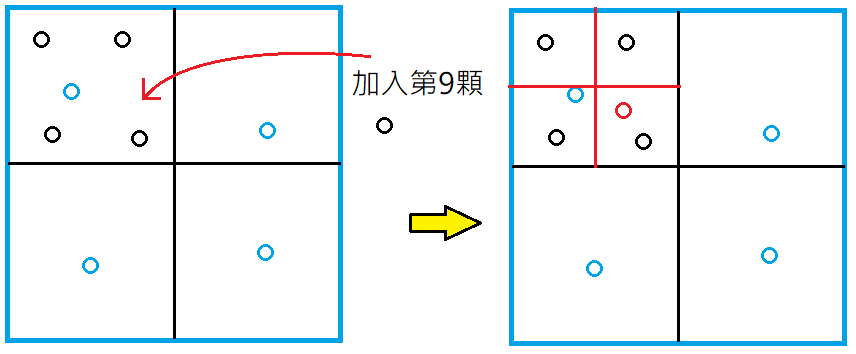
以此類推，當要放入第9顆物體時，發現黑色區域也滿了，所以就再往下分割紅色區域，並放入離該物體最近的右下角區域中，如下圖:

 

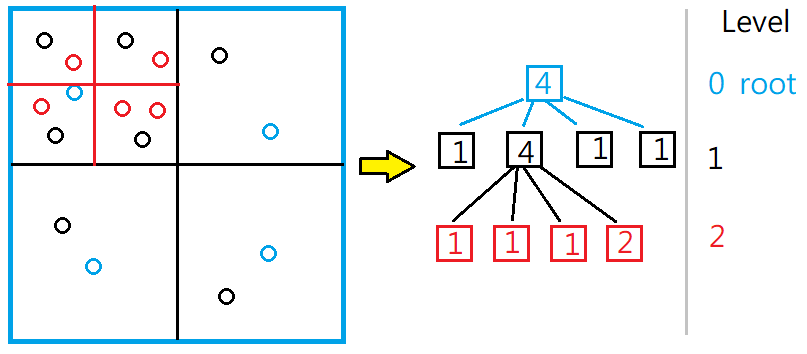
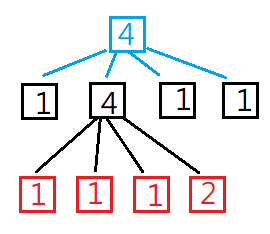
最後，就可以得出這樣的樹狀結構，這就是為什麼會叫做4叉樹的原因，如下圖:

 

搜尋流程:

給定一搜尋範圍，並逐一排除不可能的區域，最後取得搜尋範圍內的物體。

 

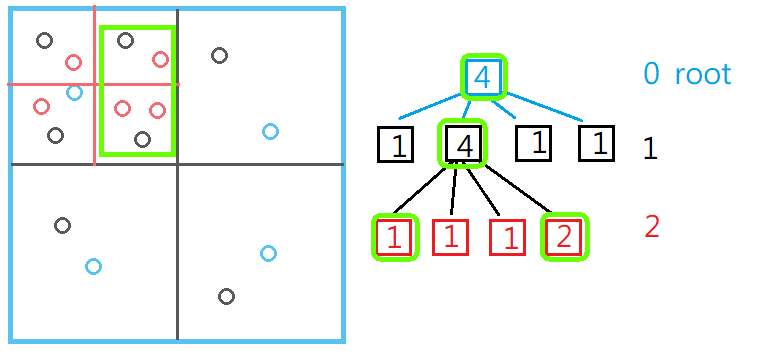
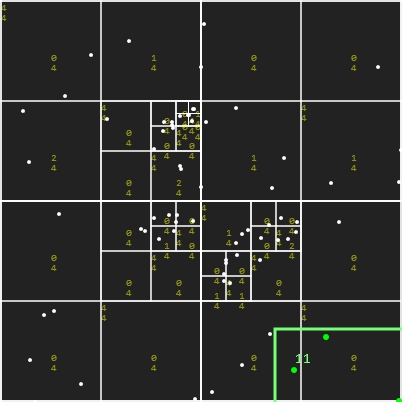
接續前面插入的狀態，假設我要檢測綠色框框內的物體是否發生碰撞，步驟如下 :

  1. 與藍框區域作碰撞檢測，發現有所交集，檢測藍色區域的物體是否包含在綠框中，發現並沒有。
  2. 與藍框的黑色子區域作檢測，發現只與左上的區域有所交集，所以排除另外三個區域，並發現有2個物體包含在綠框內。
  3. 再往下檢察左上黑框的紅色子區域，並排除左上、左下，發現有3個物體在綠框內，紅框沒有子領域，走訪結束。

最後回傳搜尋到的5個物體。

 

 

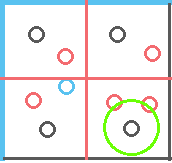
如果是碰撞檢測的應用的話，就是把綠框換成該物體周圍可能發生碰撞的範圍，再來套入搜尋，就能更加簡化碰撞檢測的流程，如下圖 :

假設要檢查有機會與黑色物體碰撞的物體，透過上述的篩選流程，最後只要針對與綠框相交的2個紅色物體，來執行碰撞檢測，以此達成碰撞效率優化。

 

這就是四叉樹的原理，接著進入實作環節吧。

 

實作QuadTree – 插入

先整理大致的插入順序:

  1. 如果該點不屬於A區域，直接結束
  2. 如果該點屬於A區域，且A區域容量還夠的時候，將該點加入A區域
  3. 如果A區域容量不夠時，將A區域劃分4個子區域，並將該點加入離它最近的子區域

 

建立基本物件 :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// ----------------------------------------
class Point {
    constructor(x, y) {
        this.collisionType = "point";
        this.x = x;
        this.y = y;
    }
}
 
class Rect {
    constructor(x, y, w, h) {
        this.collisionType = "rect";
        this.x = x;
        this.y = y;
        this.w = w;
        this.h = h;
    }
}

 

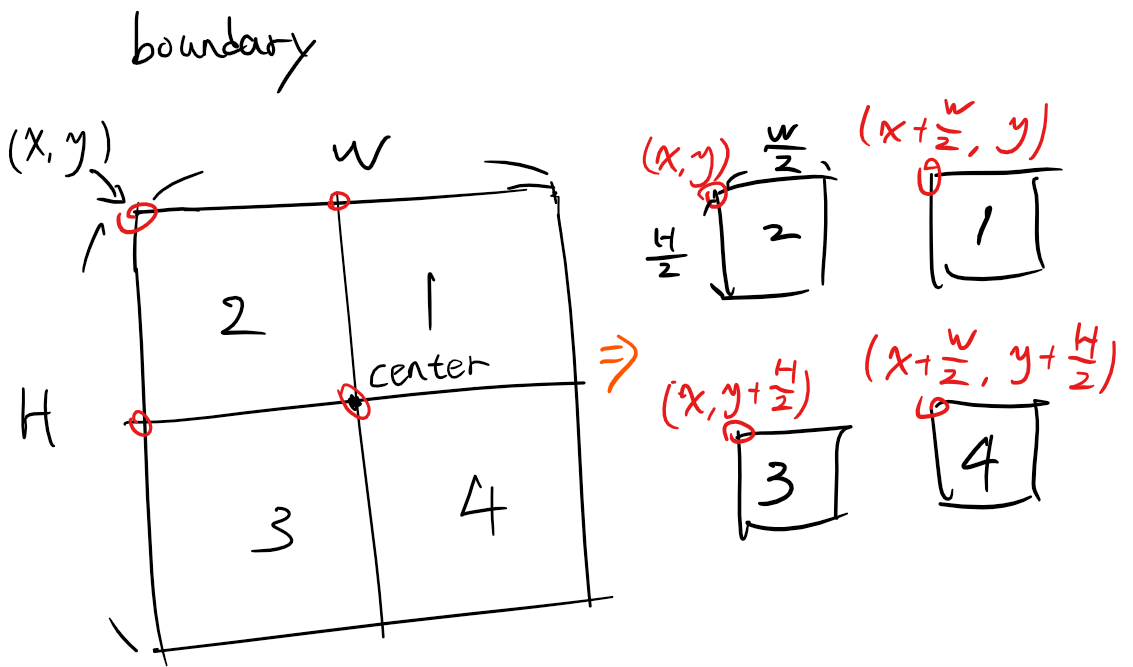
四個子區域的規劃:

並依照前述所說的插入順序，來建立QuadTree :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
// ----------------------------------------
class QuadTree {
    constructor(boundary, level) {
        this.MAX_OBJ = 4;// 該容器最大容量
        this.MAX_LEVEL = 5;// 最大深度
 
        this.objs = [];// 該容器的物體集合
        this.areas = [];// 四塊子區域
        this.level = level || 1;//當前深度
 
        this.boundary = boundary;// 容器範圍(Rect)
    }
 
    /*
    如果該點在範圍內，且容量也夠的話就新增該點至區域內，或是到達最大深度也直接新增
    到達容量上限後，就分割出四個子領域，再將物體分類至最靠近的子領域中
    */
    insert(object) {
        // 先確認物體是否在邊界內
        if (!CheckCollision(this.boundary, object)) return false;
 
        // 如果當前容量與深度未達上限，就直接新增該物體
        if (this.objs.length < this.MAX_OBJ || this.level >= this.MAX_LEVEL) {
            this.objs.push(object);
            return true;
        }
        
        // 如果容量達上限，且沒有子領域的話，分割出四個子領域
        if (this.areas.length <= 0) this.subdivide();
 
        // 嘗試給子領域新增該物體
        for (let area of this.areas) {
            if (area.insert(object)) return true;
        }
    }
 
    subdivide() {
        let x = this.boundary.x, y = this.boundary.y;
        let w = this.boundary.w, h = this.boundary.h;
 
        // 矩形以左上為基準，依照各象限順序建立子領域，並新增到areas中
        this.areas.push(new QuadTree(new Rect(x + w / 2, y, w / 2, h / 2), this.level + 1));// topRight
        this.areas.push(new QuadTree(new Rect(x, y, w / 2, h / 2), this.level + 1));// topLeft
        this.areas.push(new QuadTree(new Rect(x, y + h / 2, w / 2, h / 2), this.level + 1));// bottomLeft
        this.areas.push(new QuadTree(new Rect(x + w / 2, y + h / 2, w / 2, h / 2), this.level + 1));// bottomRight
    }
 
    show(ctx) {
        // 繪製邊界
        ctx.strokeStyle = "#FFF";
        ctx.strokeRect(this.boundary.x, this.boundary.y, this.boundary.w, this.boundary.h);
 
        // 顯示物體數/容量數，Debug
        drawString(ctx, this.objs.length + "\n" + this.MAX_OBJ,
            this.boundary.x + this.boundary.w / 2, this.boundary.y + this.boundary.h / 2,
            "rgba(255,255,0,0.5)", 10, "consolas",
            0, 0, 0);
 
        // 往下繪製所有子領域區塊
        if (this.areas.length != 0) {
            for (let area of this.areas) {
                area.show(ctx);
            }
        }
 
        // 繪製出這塊領域的物體
        for (let obj of this.objs) {
            ctx.beginPath();
            ctx.arc(obj.x, obj.y, 3, 0, Math.PI * 2);
            ctx.stroke();
        }
    }
}

至於這邊的CheckCollision(ObjectA, ObjectB)，就是單純的點與矩形的碰撞檢測，請參考結尾附上的Code。

 

使用方法 :

1
2
3
4
5
6
7
8
9
// 建立QuadTree
var qt = new QuadTree(new Rect(0, 0, Width, Height));
 
// 新增物體
qt.insert(new Point(X, Y));
 
// 在Canvas中顯示分割與物體狀況
qt.show(Context);
// ----------------------------------------

如此一來就能建立基本可新增物體的QuadTree了。

 

基本插入範例，滑鼠點擊即可新增物體。新視窗執行 : Here .

然後可以看到，每當一個區域插入4個物體後(MAX_OBJ = 4)，就會將該領域往下分割4個子區域，最多分割5層(MAX_LEVEL = 5)。

 

實作QuadTree – 搜尋

搜詢的大致順序 :

  1. 如果搜尋範圍跟當前領域相交，檢查該領域有多少物體包含在搜尋範圍中，並增加至陣列中
  2. 當該領域有子區域時，繼續往下檢查有多少物件包含在搜尋範圍內
  3. 直到所有搜尋範圍內的區域都被檢測過，回傳所有在搜尋範圍內的物體

可以比對一下上面講的搜尋流程，應該會更清楚。

 

根據上述步驟，在QuadTree中加入query這個function :

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
// ----------------------------------------
query(range, found){
    // 如果沒有給定回傳的陣列，就建立一個
    if(!found) found = [];
 
    // 判斷搜尋範圍(range)是否與當前領域有相交，沒有就直接跳掉，以節省效率
    if (!CheckCollision(this.boundary, range)) return;
 
    // 如果搜尋範圍跟當前領域相交，檢查該領域有多少物體包含在搜尋範圍中，並增加至found
    for(let p of this.objs){
        if (CheckCollision(p, range)){
            found.push(p);
        }
    }
    
    // 當該領域有子區域時，繼續往下檢查有多少物件包含在搜尋範圍內
    if(this.areas.length != 0){
        for(let area of this.areas){
            area.query(range, found);
        }
    }
 
    // 完成搜尋，回傳結果
    return found;
}

而使用方法也非常簡單，給定一個搜尋區域，接著query就會直接撈出所有在搜尋範圍內的物體了 :

1
2
3
4
5
6
7
8
9
10
// ----------------------------------------
// 假設queryTree已經新增一些物體了
 
// 建立一個搜尋範圍
var checkRange = new Rect(20, 40, 150, 150);
 
// 套用搜尋範圍至queryTree取得範圍內的物體
var objects = queryTree.query(checkRange);
 
// ----------------------------------------

 

 

基本搜尋範例，滑鼠點擊新增物體，移動可取得範圍內的物體。新視窗執行 : Here .

 

實際應用

我將正常的碰撞檢測與QuadTree檢測放在一起做比較，可以清楚的看到，當物體數量到2000時，No QuadTree的檢測方法已經無法負荷，畫面有明顯卡頓。換成QuadTree檢測後，就只掉一點FPS，透過比對，可以明顯看到效能的提升。

 

每當物體碰撞時變成白色，滑鼠點擊新增100個物體，按下按鈕以切換不同檢測模式，觀察效能的差距 :

在新視窗執行 : Here .

 

總結

QuadTree或許不是最好的多物體檢測法，但多數狀況下還堪用，至於QuadTree優化的部分，可以參考這篇文章，講得非常清楚。

這邊預計要再補上QuadTree跟其他檢測法的優缺點，但目前只研究QuadTree，所以無從比較，日後補上。

 

文章中所有的Source Code都在article中 : https://github.com/md9830415/JS-QuadTree

 

大概就是這樣了，下期再見，掰掰。

 

 

參考資源、延伸閱讀

Coding Challenge #98.1: Quadtree – Part 1

Quick Tip: Use Quadtrees to Detect Likely Collisions in 2D Space

Efficient (and well explained) implementation of a Quadtree for 2D collision detection

JavaScript QuadTree Implementation

WIKI Quadtree

 

 

發佈留言

發佈留言必須填寫的電子郵件地址不會公開。 必填欄位標示為 *