1. 前言
先來簡單的介紹一下什麼是8-Puzzle。
數字推盤遊戲(n-puzzle)是最早一種的滑塊類遊戲,常見的類型有十五數字推盤遊戲和八數字推盤遊戲等,也有以圖畫代替數字的推盤遊戲。
如上圖所示,滑塊只能往空位移動。
大概了解遊玩方法後,就來試著解決8-Puzzle問題吧!
解法的步驟大概是這樣 :
- 先完成移動判斷和節點狀態的儲存結構
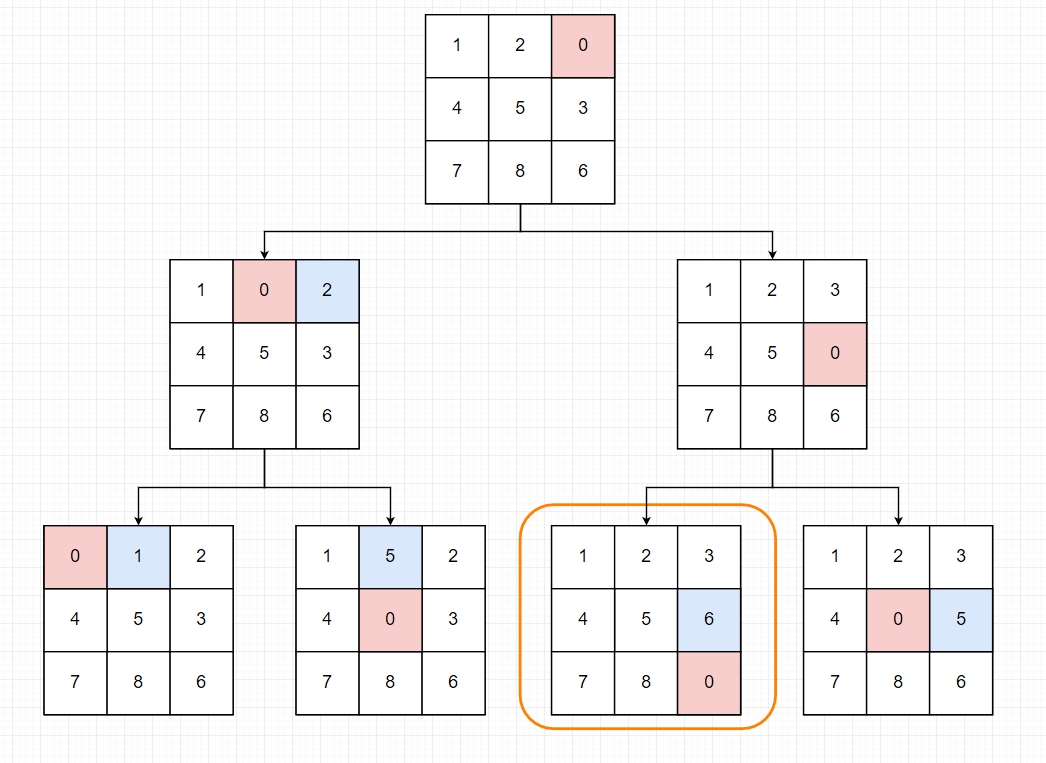
- 用BFS窮舉狀態,並把當前狀態記錄下來篩選重複路徑
- 只要有一組路徑符合結果,該路徑就是最佳解(因BFS的特性是每次平均向外擴展,所以最先碰到終點的就是最佳解之一)
- 否則搜尋完畢後皆沒有找到符合的狀態,無解
- 最後透過父節點的回溯取得輸出路徑,即可得到最短路徑和分解步驟
2. 儲存結構和移動判斷
首先是儲存狀態,用二維陣列來儲存比較直觀,但是用一維陣列來儲存的話,我覺得在一些處理上比較方便,所以我採用一維陣列。
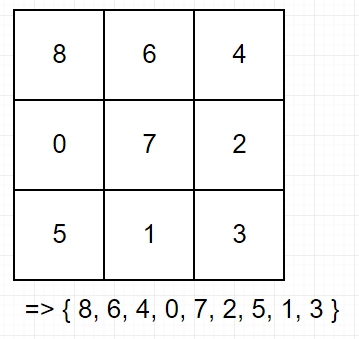
像是上面的這個狀態這樣,將0表示為空格,可以儲存成 { 8, 6, 4, 0, 7, 2, 5, 1, 3}。
因為要透過BFS搜尋來取得路徑,所以需要建立一個節點的結構,這樣才能儲存當前狀態,並紀錄上個狀態 :
public class Node
{
public byte[] status; // 當前狀態
public Node father; // 紀錄上個狀態,如果father = null 該點為根節點
public Node(byte[] status, Node father)
{
this.status = status;
this.father = father;
}
// 把陣列轉換成數字序列,比對時就不用兩將陣列元素一一檢查了
// 像是 stauts = {8, 6, 4, 0, 7, 2, 5, 1, 3},轉後後即可得到864072513
public int ToToSequence()
{
int result = 0;
for (int i = 0; i < status.Length; i++)
result = result * 10 + status[i];
return result;
}
}
再來是移動判斷,滑塊在移動時,可以看成是空白方塊在移動。
如上圖,0 可以往上、右、下移動,但是不能往左,那麼要如何判斷0能往哪個方向走呢?
如上圖,當 index = 3 時,可以得知在二維時座標是 (0, 1)。
能取得對應位置後,就能夠寫出移動判斷,像是當空位在最左邊時Col = 0,那麼就不能往左走,因為在最左邊了,在最下面時Row = 2,不能往下走,因為已經到底了。
所以可以得出:
- Col != 0,可以往左走
- Col != 2,可以往右走
- Row != 0,可以往上走
- Row != 2,可以往下走
但是只有判斷能不能走還不夠,因為當空格移動時,必須跟那個位置的數字交換,並記錄下原本的狀態 :
List<Node> GetNext(Node now)// 傳入當前版面,回傳0所有移動後的狀態
{
int index = Array.IndexOf<byte>(now.status, 0);
int col = index % 3;
int row = index / 3;
List<Node> nextPush = new List<Node>();
byte[] next;
if (row != 0) // Top
{
next = (byte[])now.status.Clone();
swap(ref next[index], ref next[index - 3]);// 跟上面交換
nextPush.Add(new Node(next, now));// 加入這個新狀態
}
if (col != 2) // Right
{
next = (byte[])now.status.Clone();
swap(ref next[index], ref next[index + 1]);// 跟右邊交換
nextPush.Add(new Node(next, now));
}
if (row != 2) // Bottom
{
next = (byte[])now.status.Clone();
swap(ref next[index], ref next[index + 3]);// 跟下面交換
nextPush.Add(new Node(next, now));
}
if (col != 0) // Left
{
next = (byte[])now.status.Clone();
swap(ref next[index], ref next[index - 1]);// 跟左邊交換
nextPush.Add(new Node(next, now));
}
return nextPush;
}
在交換前要先複製一份,因為陣列參數是傳參考,直接交換會修改到原本的狀態,所以要先Clone後再傳給新狀態做交換。
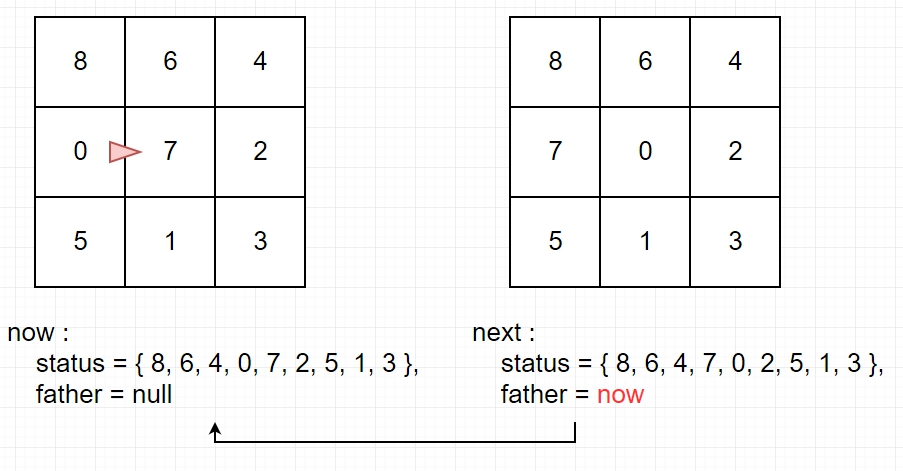
而上面程式碼中 new Node(next, now),意思是建立一個新節點next,而他的前一個狀態是剛剛傳進來的now。
如上圖,假設now是根結點,而next是下個節點,那麼new Node(next, now)後就會像這樣。
3. 用BFS窮舉狀態
有了移動判段後,接下來的解法就跟用BFS解迷宮差不多了 :
// 傳入原本的版面和目標版面,回傳最短路徑
List<Node> Solve(byte[] source, byte[] goal)
{
Queue<Node> queue = new Queue<Node>();
// 使用狀態序列來儲存已走過的路徑,防止往回走
SortedList<int, bool> book = new SortedList<int, bool>();
Node end = new Node(goal, null);// 終點
Node start = new Node(source, null);// 起點
queue.Enqueue(start);// 推入起點
book.Add(start.ToSequence(), true);// 標示起點已走過,防止走回頭路
int endStatus = end.ToSequence();
while (queue.Count > 0)
{
// 取得當前搜索狀態,並移出佇列
Node now = queue.Dequeue();
// 如果抵達終點,那就輸出路徑
if (now.ToSequence() == endStatus)
return PathTrace(now);
// 取得能走的位置
List<Node> nextPath = GetNext(now);
foreach (var path in nextPath)
{
int sign = path.ToSequence();
// 判斷當前節點狀態是否擴展過了
if (!book.Keys.Contains(sign))
{
// 推入當前狀態,並標記該路徑已走過,因為每個狀態只需要擴展一次就夠了
queue.Enqueue(path);
book.Add(sign, true);
}
}
}
// 如果窮舉完都沒找到,代表無解
return null;
}
List<Node> PathTrace(Node now)
{
// 回朔路徑
List<Node> path = new List<Node>();
while (now.father != null)
{
path.Add(now);
now = now.father;
}
path.Reverse();
return path;
}
路徑的儲存使用SortedList而不是正常的List,因為List在加入物件時並不會特別處理,所以在搜尋時就只能慢慢比較,而 SortedList的結構類似二元搜尋樹,在新增資料時就會依照設定的Key值做排序後再插入,所以在搜尋時的複雜度就能夠降到O(log2 n),想了解更多的話請看最後的參考資源。
到這邊大概就能了解為什麼要用ToSequence()來儲存路徑了,因為資料不會重複,所以搭配SortedList就比List快的多。
使用方法:
byte[] source = new byte[] { 8, 6, 4, 0, 7, 2, 5, 1, 3 };
byte[] goal = new byte[] { 1, 2, 3, 4, 5, 6, 7, 8, 0 };
List<Node> path = Solve(source, goal);
Console.WriteLine($"最少步驟為:{path.Count}");
給定原本面狀態跟輸出狀態,即可得到最短路徑的List,而輸出路徑只要走訪一遍Path即可得到。
其實執行的原理很簡單,就是一直窮舉所有狀態,直到符合結果為止
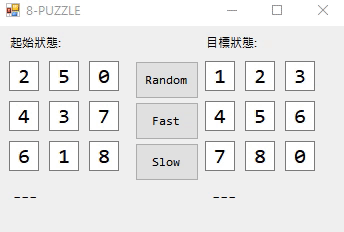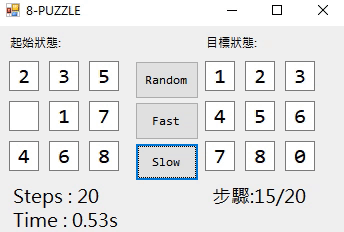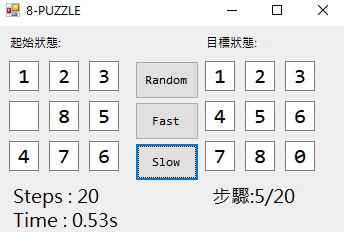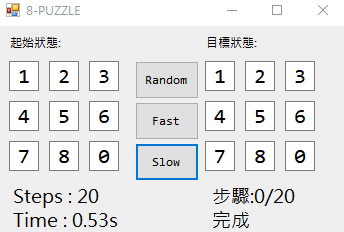
4. 執行結果
Source Code : Here
雖然用BFS就能解了,但效率很差,之後會再研究看看A*演算法。