定義
平面三角形T有A、B、C頂點,而內部的任一點P,都可以透過$\overrightarrow{AB}$與$\overrightarrow{AC}$的線性組合來表示,所以P點表示法如下:
$$ \overrightarrow{AP}=u\overrightarrow{AB}+v\overrightarrow{AC} $$
將它分解整理後: $$ P-A=u(B-A)+v(C-A) $$
最終得到: $$ P(x,y) = (1-u-v)A + uB + vC~,~~0\leq u,v\leq 1$$
如果將A、B、C的三個係數換一下,就變成:
$$ P(x,y)= \alpha A + \beta B +\gamma C~,~~\alpha+\beta+\gamma=1 $$
而這就是重心座標的表示法,透過 $[\alpha,\beta,\gamma]$ 這三個介於[0,1]之間的係數,來決定P在三角形內部的相對位置
實際範例: Barycentric coordinates of a point
首先第一個問題就是,有了三角形ABC與內部的P點,要怎麼求出對應的係數?
推導方式 1. 外積
將原式改寫,可以把P點看成是起點為A,透過$\overrightarrow{AB},\overrightarrow{AC}$為基底的座標為$(u,v)$: $$ P = A + u\overrightarrow{AB}+v\overrightarrow{AC} $$ 找到滿足此條件的$u,v$ $$ u\overrightarrow{AB}+v\overrightarrow{AC}+\overrightarrow{PA} = 0 $$ 平面三角形的座標拆開成$(x,y)$分量
$$ \begin{cases} u\overrightarrow{AB}.{x} + v\overrightarrow{AC}.{x} + \overrightarrow{PA}.{x} = 0 \\ u\overrightarrow{AB}.{y} + v\overrightarrow{AC}.{y} + \overrightarrow{PA}.{y} = 0 \end{cases} $$
以矩陣表示: $$ \begin{cases} \begin{bmatrix}u & v & 1 \end{bmatrix} \begin{bmatrix} \overrightarrow{AB}.{x} \\ \overrightarrow{AC}.{x} \\ \overrightarrow{PA}.{x} \end{bmatrix}=0 \\ \\ \begin{bmatrix}u & v & 1 \end{bmatrix} \begin{bmatrix} \overrightarrow{AB}.{y} \\ \overrightarrow{AC}.{y} \\ \overrightarrow{PA}.{y} \end{bmatrix}=0 \end{cases} $$
可以發現兩條式子的點積都為0,表示$[u,v,1]$這個向量,同時垂直於$x$分量與$y$分量,這就代表$[u,v,1]$剛剛好就是x分量與y分量的外積(Cross)
另變數 uv 為$[u,v,c]$ = $(\overrightarrow{AB}.{x} , \overrightarrow{AC}.{x} , \overrightarrow{PA}.{x}) \times (\overrightarrow{AB}.{y} , \overrightarrow{AC}.{y} , \overrightarrow{PA}.{y})$ 的結果
但這裡要注意的是,uv得到的外積結果,僅僅是方向正確,確實垂直於x與y分量的向量,但大小卻不一定正確,不過 $c$ 的值已經知道是1了,所以只要讓uv的值要再進行縮放,讓 $c = 1$ 就是正確的 $uv$
將$[u,v,c]$帶回: $$ u\overrightarrow{AB}+v\overrightarrow{AC}+c\overrightarrow{PA} = 0 $$
$c$ 的值應該要為1,同除以 $c$ 得到: $$ \frac{u}{c}\overrightarrow{AB}+\frac{v}{c}\overrightarrow{AC}+\overrightarrow{PA} = 0 $$ 展開將P拿出來,最終得到完整式子: $$ P = (1-\frac{u}{c}-\frac{v}{c})A + \frac{u}{c}B + \frac{v}{c}C~,~~c\neq 0 $$
也就是: $$ P= \alpha A + \beta B +\gamma C~,~~\alpha+\beta+\gamma=1 $$ 其中: $$ \begin{cases} & \alpha=1-\frac{u}{c}-\frac{v}{c} \\ & \beta= \frac{u}{c} \\ & \gamma= \frac{v}{c} \end{cases} $$
程式碼:
// 透過外積法計算向量座標
Vec3f barycentric(Vec2f A, Vec2f B, Vec2f C, Vec2f P) {
// Vec3f [x,y,z] = [u,v,c]
Vec3f vec_x(B.x - A.x, C.x - A.x, A.x - P.x); // vAB.x,vAC.x,vPA.x
Vec3f vec_y(B.y - A.y, C.y - A.y, A.y - P.y); // vAB.y,vAC.y,vPA.y
Vec3f uv = cross(vec_x, vec_y);
// 不得除以0,做個檢查,因為浮點數可能會有誤差,所以給定一個範圍
if (std::abs(uv[2]) > 1e-2){
float alpha = 1.f - (uv.x + uv.y) / uv.z;
float beta = uv.y / uv.z;
float gamma = uv.x / uv.z;
return Vec3f(alpha, beta, gamma);
}
// uv.z為0的狀況為異常,傳回不符合定義的值,讓rasterizator捨棄這個點
return Vec3f(-1, 1, 1); //通常不會發生
}
推導方式 2. 面積比
$\alpha, \beta ,\gamma$ 為A,B,C頂點對邊的面積比,詳細證明待補,面積比有兩種大致的推導方法:
- 直接行列式求面積去算$\alpha$=Area(BPC)/AREA(ABC) 參考
- 找出AC邊的法向量N,將AP投影到N上,即可得到AC到P點的高,而底邊就是|AC|,將高乘以底邊就是Area(APC)的面積,剩下就一樣求出面積比
1.的方法很直觀不用推了,簡單推導2.的方法:
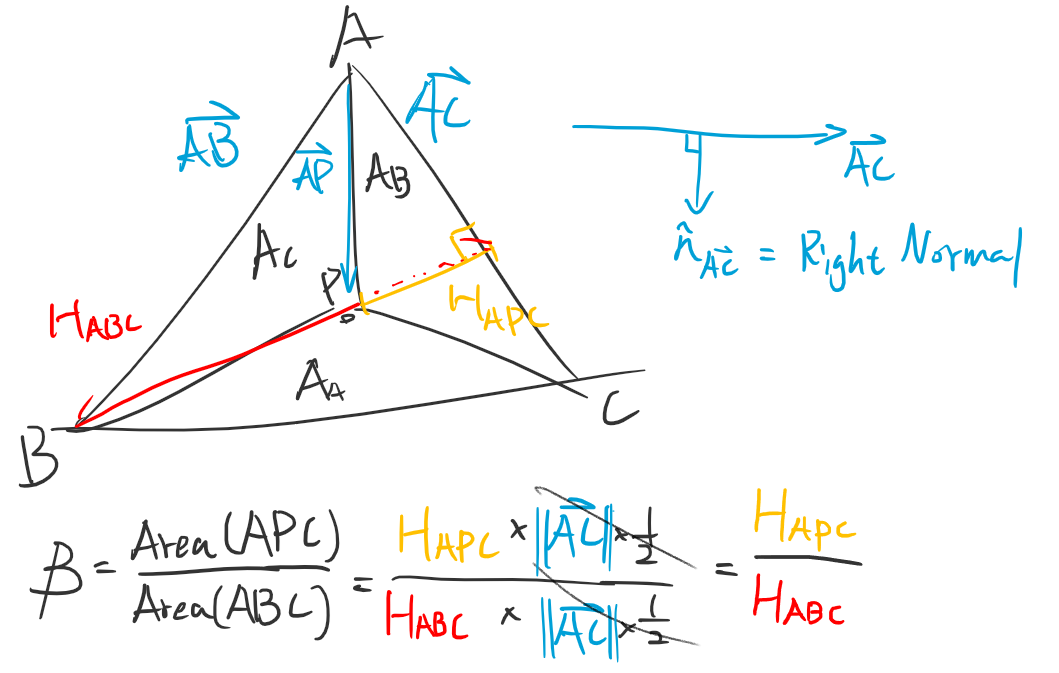
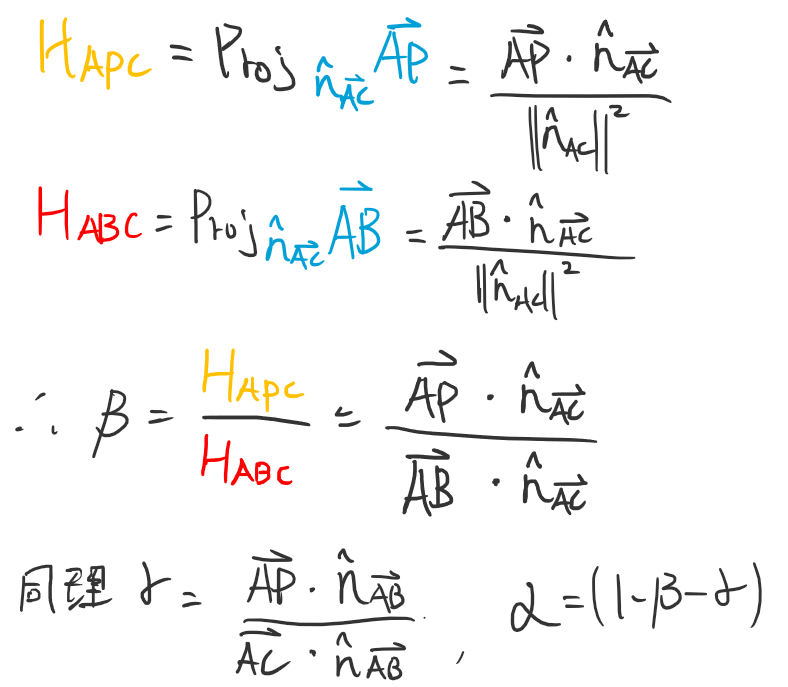
$$ P= \alpha A + \beta B +\gamma C~,~~\alpha+\beta+\gamma=1 $$
// 透過面積計算重心座標
Vec3f barycentric(Vec2f A, Vec2f B, Vec2f C, Vec2f P) {
auto ab = B - A;
auto ac = C - A;
auto ap = p - A;
Vec2f nac(A.y - C.y, - A.x + C.x);
Vec2f nab(A.y - B.y, - A.x + B.x);
float beta = (ap * nac) / (ab * nac); // operator* is dot
float gamma = (ap * nab) / (ac * nab);
float alpha = 1.f - beta - gamma;
return Vec3f(alpha, beta, gamma);
}
基本使用
基本轉換:
-
已知三頂點A,B,C位置與絕對位置P點,要如何得出相對位置的比例參數 $[\alpha,\beta,\gamma]$ ?
直接帶入前面完成的bary函式bary(A,B,C,P),得到計算後傳回的 $[\alpha,\beta,\gamma]$ -
已知A,B,C頂點與相對位置參數 $[\alpha,\beta,\gamma]$ 或是 $[u,v]$,如何得到絕對位置P點?
直接將參數與頂點代入定義即可:
$ P= \alpha A + \beta B +\gamma C $
$ P= (1-u-v)A + uB + vC $
應用方式
紋理貼圖:
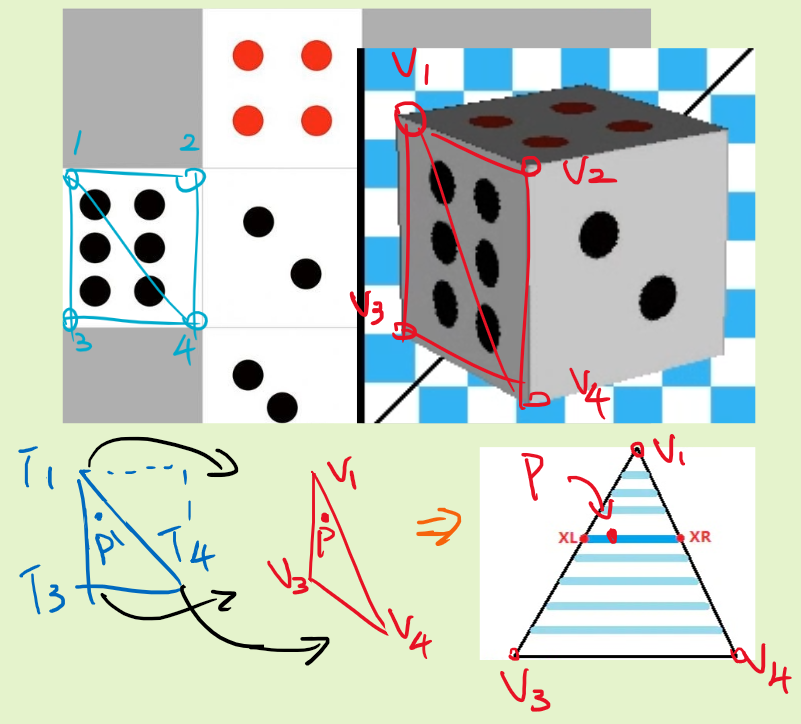
如上圖,希望能將左邊藍色的貼圖,映射到右邊的紅色模型上,這過程稱為紋理貼圖或是貼皮,而此時會有幾個問題
- 紅色三角形已經過座標變換,掃描線準備上色時會有一個動點P,如何知道三角形中所有P點對應的貼圖顏色?
- 兩片三角形已經大不相同,要如何在不影響圖形比例的情況將其著色?
掃描線的動畫圖解: Rasterizer Algorithm Explanation
大略步驟:
- 透過Barycentric(V1, V3, V4, P),得到P點在紅色三角形的相對位置(u, v)
- 帶入貼圖三角形T中 $P'= (1-u-v)T_{1} + u~T_{2} + v~T_{4}$ 取得$P'$點座標,也就能取得貼圖於P(x,y)的顏色
- 最後就能取得紅色P點對應的貼圖顏色,如此反覆將P隨著掃描線計算,即可取得整片三角形的貼圖對應
重複此過程渲染兩片三角形後,就能將骰子點數6的這一面印出
結論
暫無,之後再補